Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T06:33:14.219Z Has data issue: false hasContentIssue false
  • English
  • Français

Cardinalities of locally compact groups and their Stone-Čech compactifications

Published online by Cambridge University Press:  17 April 2009

Gerald L. Itzkowitz ,
Sidney A. Morris  and
Vladimir V. Tkachuk
Gerald L. Itzkowitz
Affiliation:
Department of Mathematics, Queens College, The City University of New York, Flushing, N.Y., 11367, United States of America e-mail: [email protected]
Sidney A. Morris
Affiliation:
School of Information Technology and Mathematical Sciences, University of Ballarat, P.O. Box 663, Ballarat, Vic. 3353, [email protected]
Vladimir V. Tkachuk
Affiliation:
Departmento de Matemáticas, Universidad Autónoma Metropolitana, Av. San Rafael Atlixco, 186, Col. VicentinaIztapalapa, C.P. 09340México D.F., e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Dedicated to Edwin Hewitt

If G is any Hausdorff topological group and βG is the Stone-Čech compactification then 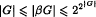where |G| denotes the cardinalty of G It is known that if G is a discrete group then 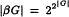and if G is the additive group of real numbers with the Euclidean topology, then |βG| = 2|G|. In this paper the cardinality and weight of βG, for a locally compact group G, is calculated in terms of the character and Lindelöf degree of G The results make it possible to give a reasonably complete description of locally compact groups G for which |βG| = 2|G| or even |βG| = |G|.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 67 , Issue 3 , June 2003 , pp. 353 - 364
Copyright
Copyright © Australian Mathematical Society 2003

References

[1]Arhangel'skii, A.V., Topological function spaces (Kluwer Acad. Publ. Dordrecht, 1992).CrossRefGoogle Scholar
[2]Cleary, J. and Morris, S.A., ‘Topologies on locally compact groups’, Bull. Austral. Math. Soc. 38 (1988), 105–111.CrossRefGoogle Scholar
[3]Cleary, J. and Morris, S.A., ‘Locally dyadic topological groups’, Bull. Austral. Math. Soc. 40 (1989), 417–419.CrossRefGoogle Scholar
[4]Cleary, J. and Morris, S.A., ‘Compact groups and products of the unit interval’, Math. Proc. Cambridge Philos. Soc. 110 (1991), 293–297.CrossRefGoogle Scholar
[5]Comfort, W.W., Topological groups, Handbook of set-theoretic topology (Elsevier Science Publishers, B.V., 1984), pp. 1143–1263.Google Scholar
[6]Comfort, W.W. and Ross, K.A., ‘Pseudocompactness and uniform continuity in topological groups’, Pacific J. Math. 16 (1966), 483–496.CrossRefGoogle Scholar
[7]Engelking, R., General topology (PWN, Warszawa, 1977).Google Scholar
[8]Gillman, L. and Jerison, M., ‘Rings of continuous functions’ (D. van Nostrand Company Inc., Princeton, N.J.).CrossRefGoogle Scholar
[9]Hodel, R., Cardinal functions I, Handbook of Set-Theoretic Topology (Elsevier Science Publishers, B.V., 1984), pp. 1–61.Google Scholar
[10]Hofmann, K.H. and Morris, S.A., The structure of compact groups. A primer for the student — a handbook for the expert, de Gruyter Studies in Math. 25 (Walter de Gruyter and Co., Berlin, 1998).Google Scholar
[11]Hofmann, K.H. and Morris, S.A., ‘The structure of pro-Lie groups and locally compact groups’, (to appear). (See http://www.ballarat.edu.au/~smorris/loccocont.pdf).Google Scholar
[12]Hewitt, E. and Ross, K.A., Abstract harmonic analysis, Vol. I (Springer-Verlag, Berlin, 1963).Google Scholar
[13]Itzkowitz, G.L., ‘On the density character of compact topological groups’, Fund. Math. 75 (1972), 201–203.CrossRefGoogle Scholar
[14]Kuz'minov, V., ‘On a hypothesis of P.S. Alexandroff in the theory of topological groups’, Dokl. Acad. Nauk SSSR, Natural Sciences 125 (1959), 727–729.Google Scholar
[15]Shapirovsky, B.E., ‘on imbedding extremally disconnected spaces in compact Hausdorff spaces, b-points and weight of pointwise normal spaces’, Soviet Math. Dokl. 16 (1975), 1056–1061.Google Scholar