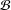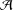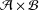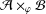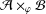Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ABTAHI, F.
and
GHAFARPANAH, A.
2015.
A NOTE ON CYCLIC AMENABILITY OF THE LAU PRODUCT OF BANACH ALGEBRAS DEFINED BY A BANACH ALGEBRA MORPHISM.
Bulletin of the Australian Mathematical Society,
Vol. 92,
Issue. 2,
p.
282.
CHOI, YEMON
2016.
TRIVIALITY OF THE GENERALISED LAU PRODUCT ASSOCIATED TO A BANACH ALGEBRA HOMOMORPHISM.
Bulletin of the Australian Mathematical Society,
Vol. 94,
Issue. 2,
p.
286.
Pourabbas, A.
and
Razi, N.
2016.
Some homological properties of $${T}$$ T -Lau product algebras.
Acta Mathematica Hungarica,
Vol. 149,
Issue. 1,
p.
31.
Pourmahmood Aghababa, Hasan
and
Shirmohammadi, Nematollah
2017.
On amalgamated Banach algebras.
Periodica Mathematica Hungarica,
Vol. 75,
Issue. 1,
p.
1.
Dabhi, Prakash A
and
Patel, Savan K
2017.
Spectral properties and stability of perturbed Cartesian product.
Proceedings - Mathematical Sciences,
Vol. 127,
Issue. 4,
p.
673.
Ramezanpour, Mohammad
2018.
More on cyclic amenability of the Lau product of Banach algebras defined by a Banach algebra morphism.
Mathematica Slovaca,
Vol. 68,
Issue. 1,
p.
147.
Ebadian, A.
and
Jabbari, A.
2019.
ГИПЕРТАУБЕРОВЫ АЛГЕБРЫ, ОПРЕДЕЛЕННЫЕ ГОМОМОРФИЗМОМ БАНАХОВОЙ АЛГЕБРЫ.
Вестник КРАУНЦ. Физико-математические науки,
p.
18.
Lakzian, Hosein
and
Barootkoob, Sedigheh
2021.
Biprojectivity and Biflatness of Bi-amalgamated Banach Algebras.
Bulletin of the Iranian Mathematical Society,
Vol. 47,
Issue. 1,
p.
63.
Dabhi, Prakash A.
Patel, Savan K.
and
Pipaliya, Yuvraj D.
2023.
On various spectra of elements of $${\mathcal {A}} \times _\theta {\mathcal {B}}$$.
The Journal of Analysis,
Vol. 31,
Issue. 1,
p.
855.
Valaei, Mohammad
and
Zıvarı-kazempour, Abbas
2024.
Spectrum, homomorphisms and multipliers of Lau product of Banach algebras.
Hacettepe Journal of Mathematics and Statistics,
Vol. 53,
Issue. 3,
p.
777.
Barootkoob, S.
and
Lakzian, H.
2024.
Some homological properties on generalized amalgamated Banach algebras.
Filomat,
Vol. 38,
Issue. 4,
p.
1401.