Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
LIN, JING
ZENG, QINGHOU
and
CHEN, FUYUAN
2019.
MAXIMUM CUTS IN GRAPHS WITHOUT WHEELS.
Bulletin of the Australian Mathematical Society,
Vol. 100,
Issue. 1,
p.
13.
Ma, Huawen
2020.
Maximum Cuts in $$\mathscr {H}$$-Free Graphs.
Graphs and Combinatorics,
Vol. 36,
Issue. 5,
p.
1503.
Carlson, Charles
Kolla, Alexandra
Li, Ray
Mani, Nitya
Sudakov, Benny
and
Trevisan, Luca
2021.
Lower Bounds for Max-Cut in $H$-Free Graphs via Semidefinite Programming.
SIAM Journal on Discrete Mathematics,
Vol. 35,
Issue. 3,
p.
1557.
Lin, Jing
and
Zeng, Qinghou
2021.
Maximum bisections of graphs without short even cycles.
Journal of Combinatorial Theory, Series A,
Vol. 180,
Issue. ,
p.
105404.
Rao, Mengjiao
Hou, Jianfeng
and
Zeng, Qinghou
2022.
Maximum bisections of graphs without cycles of length 4.
Discrete Mathematics,
Vol. 345,
Issue. 8,
p.
112914.
Wu, Shufei
and
Hou, Jianfeng
2023.
Graph partitioning: an updated survey.
AKCE International Journal of Graphs and Combinatorics,
Vol. 20,
Issue. 1,
p.
9.
Bai, Bo
Chen, Xiang
Hou, Jian-Feng
and
Zhang, Gong
2023.
On Ratio-k-Cuts of Graphs.
Journal of the Operations Research Society of China,
WU, SHUFEI
and
LI, AMIN
2023.
MAX-CUT BY EXCLUDING BIPARTITE SUBGRAPHS.
Bulletin of the Australian Mathematical Society,
Vol. 108,
Issue. 2,
p.
177.
Wu, Shufei
and
Xiong, Xiaobei
2024.
Maximum Bisections of Graphs with Girth at Least Six.
Graphs and Combinatorics,
Vol. 40,
Issue. 6,
Wu, Shufei
and
Zhong, Yuanyuan
2025.
Maximum bisections of graphs without cycles of length four and five.
Discrete Applied Mathematics,
Vol. 360,
Issue. ,
p.
209.
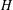 $H$-FREE GRAPHS
$H$-FREE GRAPHS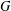 $G$, let
$G$, let 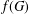 $f(G)$ denote the maximum number of edges in a bipartite subgraph of
$f(G)$ denote the maximum number of edges in a bipartite subgraph of 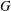 $G$. For an integer
$G$. For an integer 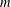 $m$ and for a fixed graph
$m$ and for a fixed graph 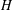 $H$, let
$H$, let 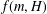 $f(m,H)$ denote the minimum possible cardinality of
$f(m,H)$ denote the minimum possible cardinality of 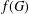 $f(G)$ as
$f(G)$ as 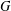 $G$ ranges over all graphs on
$G$ ranges over all graphs on 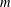 $m$ edges that contain no copy of
$m$ edges that contain no copy of 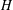 $H$. We give a general lower bound for
$H$. We give a general lower bound for 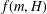 $f(m,H)$ which extends a result of Erdős and Lovász and we study this function for any bipartite graph
$f(m,H)$ which extends a result of Erdős and Lovász and we study this function for any bipartite graph 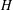 $H$ with maximum degree at most
$H$ with maximum degree at most 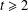 $t\geq 2$ on one side.
$t\geq 2$ on one side.