Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-17T14:18:35.546Z Has data issue: false hasContentIssue false
  • English
  • Français

BINDING NUMBER AND MINIMUM DEGREE FOR FRACTIONAL (k,m)-DELETED GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  14 October 2011

SIZHONG ZHOU ,
QIUXIANG BIAN  and
LAN XU
SIZHONG ZHOU*
Affiliation:
School of Mathematics and Physics, Jiangsu University of Science and Technology, Mengxi Road 2, Zhenjiang, Jiangsu 212003, PR China (email: [email protected])
QIUXIANG BIAN
Affiliation:
School of Mathematics and Physics, Jiangsu University of Science and Technology, Mengxi Road 2, Zhenjiang, Jiangsu 212003, PR China
LAN XU
Affiliation:
Department of Mathematics, Changji University, Changji, Xinjiang 831100, PR China
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a graph of order n, and let k≥1 be an integer. Let h:E(G)→[0,1] be a function. If ∑ e∋xh(e)=k holds for any x∈V (G), then we call G[Fh] a fractional k-factor of G with indicator function h where Fh ={e∈E(G):h(e)>0}. A graph G is called a fractional (k,m) -deleted graph if for every e∈E(H) , there exists a fractional k-factor G[Fh ] of G with indicator function h such that h(e)=0 , where H is any subgraph of G with m edges. The minimum degree of a vertex in G is denoted by δ(G) . For X⊆V (G), NG(X)=⋃ x∈XNG(x) . The binding number of G is defined by 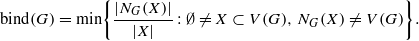In this paper, it is proved that if 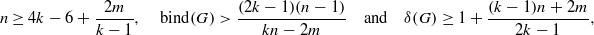then G is a fractional (k,m) -deleted graph. Furthermore, it is shown that this result is best possible in some sense.

Keywords

graphfractional k-factorfractional (k,m)-deleted graphbinding numberminimum degree

MSC classification

Secondary: 05C70: Factorization, matching, partitioning, covering and packing
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 85 , Issue 1 , February 2012 , pp. 60 - 67
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2011

Footnotes

This research was supported by Natural Science Foundation of the Higher Education Institutions of Jiangsu Province (10KJB110003) and Jiangsu University of Science and Technology (2010SL101J, 2009SL154J), and was sponsored by Qing Lan Project of Jiangsu Province.

References

[1]Bondy, J. A. and Murty, U. S. R., Graph Theory with Applications (Macmillan Press, London, 1976).CrossRefGoogle Scholar
[2]Cai, J., Liu, G. and Hou, J., ‘The stability number and connected [k,k+1]-factor in graphs’, Appl. Math. Lett. 22(6) (2009), 927–931.CrossRefGoogle Scholar
[3]Fourtounelli, O. and Katerinis, P., ‘The existence of k-factors in squares of graphs’, Discrete Math. 310(23) (2010), 3351–3358.CrossRefGoogle Scholar
[4]Liu, H. and Liu, G., ‘Neighbor set for the existence of (g,f,n)-critical graphs’, Bull. Malays. Math. Sci. Soc. (2) 34(1) (2011), 39–49.Google Scholar
[5]Liu, G. and Zhang, L., ‘Toughness and the existence of fractional k-factors of graphs’, Discrete Math. 308 (2008), 1741–1748.CrossRefGoogle Scholar
[6]Matsuda, H., ‘Fan-type results for the existence of [a,b]-factors’, Discrete Math. 306 (2006), 688–693.CrossRefGoogle Scholar
[7]Yu, J., Liu, G., Ma, M. and Cao, B., ‘A degree condition for graphs to have fractional factors’, Adv. Math. (China) 35(5) (2006), 621–628.Google Scholar
[8]Zhou, S., ‘Binding number and minimum degree for the existence of fractional k-factors with prescribed properties’, Util. Math., to appear.Google Scholar
[9]Zhou, S., ‘Independence number, connectivity and (a,b,k)-critical graphs’, Discrete Math. 309(12) (2009), 4144–4148.CrossRefGoogle Scholar
[10]Zhou, S., ‘A neighborhood condition for graphs to be fractional (k,m)-deleted graphs’, Glasg. Math. J. 52(1) (2010), 33–40.Google Scholar
[11]Zhou, S., ‘Some new sufficient conditions for graphs to have fractional k-factors’, Int. J. Comput. Math. 88(3) (2011), 484–490.CrossRefGoogle Scholar
[12]Zhou, S., ‘A sufficient condition for graphs to be fractional (k,m)-deleted graphs’, Appl. Math. Lett. 24(9) (2011), 1533–1538.CrossRefGoogle Scholar
[13]Zhou, S. and Jiang, J., ‘Toughness and (a,b,k)-critical graphs’, Inform. Process. Lett. 111(9) (2011), 403–407.Google Scholar