Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T10:55:24.157Z Has data issue: false hasContentIssue false
  • English
  • Français

BINARY SIGNED-DIGIT REPRESENTATIONS IN PAPERFOLDING

Part of: Elementary number theory Sequences and sets

Published online by Cambridge University Press:  10 June 2022

BRUCE BATES ,
MARTIN BUNDER  and
KEITH TOGNETTI
BRUCE BATES*
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, Wollongong, NSW 2522, Australia
MARTIN BUNDER
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, Wollongong, NSW 2522, Australia e-mail: [email protected]
KEITH TOGNETTI
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, Wollongong, NSW 2522, Australia e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

When a page, represented by the interval 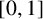$[0,1]$ , is folded right over left 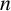$n $ times, the right-hand fold contains a sequence of points. We specify these points using two different representation techniques, both involving binary signed-digit representations.

Keywords

paperfoldingnormal additive factorisationodd-digit factorisationbinary signed-digit representation

MSC classification

Primary: 11A63: Radix representation; digital problems
Secondary: 11B85: Automata sequences
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 3 , December 2022 , pp. 363 - 375
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allouche, J.-P. and Shallit, J., Automatic Sequences: Theory, Applications, Generalizations (Cambridge University Press, Cambridge, 2003).CrossRefGoogle Scholar
Bates, B. P., Bunder, M. W. and Tognetti, K. P., ‘Locating terms in the Stern–Brocot tree’, European J. Combin. 31 (2010), 1020–1033.CrossRefGoogle Scholar
Bunder, M. W., Tognetti, K. P. and Bates, B. P., ‘Points in a fold’, Bull. Aust. Math. Soc., to appear. Published online (10 January 2022); doi:10.1017/S0004972721000897.CrossRefGoogle Scholar
Davis, C. and Knuth, D. E., ‘Number representations and dragon curves – 1’, J. Recreat. Math. 3 (1970), 66–81.Google Scholar
Dekking, F. M., France, M. Mendès and van der Poorten, A. J., ‘Folds!’, Math. Intelligencer 4 (1982), 130–138; II, ibid., 173–181; III, ibid., 190–195.CrossRefGoogle Scholar
Ebeid, N. and Hasan, M. A., ‘On binary signed digit representations of integers’, Des. Codes Cryptogr. 42 (2007), 43–65.CrossRefGoogle Scholar
France, M. Mendès and Shallit, J. O., ‘Wire bending’, J. Combin. Theory Ser. A 50 (1989), 1–23.CrossRefGoogle Scholar
France, M. Mendès and van der Poorten, A. J., ‘Arithmetic and analytical properties of paper folding sequences’, Bull. Aust. Math. Soc. 24 (1981), 123–131.CrossRefGoogle Scholar
Monroe, L., ‘Binary signed-digit integers and the Stern diatomic sequence’, Des. Codes Cryptogr. 89 (2021), 2653–2662.CrossRefGoogle Scholar
Quet, L., The Online Encyclopedia of Integer Sequences (OEIS), A119608. https://oeis.org/A119608.Google Scholar
Shallit, J., A primer on balanced binary representations. https://cs.uwaterloo.ca/~shallit/Papers/bbr.pdf.Google Scholar
Sigrist, R., The Online Encyclopeadia of Integer Sequences (OEIS), A281589. https://oeis.org/A281589.Google Scholar
Tůma, J. and Vábek, J., ‘On the number of binary signed digit representations of a given weight’, Comment. Math. Univ. Carolin. 56(3) (2015), 287–306.Google Scholar