Let s be a fixed positive integer constant and let 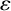$\varepsilon $ be a fixed small positive number. Then, provided that a prime p is large enough, we prove that, for any set 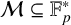${\mathcal M}\subseteq \mathbb {F}_p^*$ of size 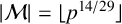$|{\mathcal M}|= \lfloor { p^{14/29}}\rfloor $ and integer 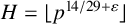$H=\lfloor {p^{14/29+\varepsilon }}\rfloor $, any integer 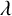$\lambda $ can be represented in the form

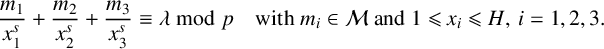$$ \begin{align*} \frac{m_1}{x_1^s}+\frac{m_2}{x_2^s}+\frac{m_3}{x_3^s}\equiv \lambda \bmod p \quad\text{with } m_i\in {\mathcal M} \text{ and } 1\leqslant x_i\leqslant H, \, i=1,2,3. \end{align*} $$

When 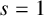$s=1$, we show that, for almost all primes p, if 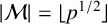$|{\mathcal M}|= \lfloor p^{1/2}\rfloor $ and 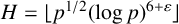$H=\lfloor p^{1/2}(\log p)^{6+\varepsilon }\rfloor $, then any integer 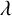$\lambda $ can be represented in the form

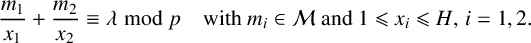$$ \begin{align*} \frac{m_1}{x_1}+\frac{m_2}{x_2}\equiv \lambda \bmod p \quad\text{with } m_i\in {\mathcal M} \text{ and } 1\leqslant x_i\leqslant H, \, i=1,2. \end{align*} $$