Published online by Cambridge University Press: 08 July 2015
Let 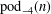 $\text{pod}_{-4}(n)$ denote the number of partition quadruples of
$\text{pod}_{-4}(n)$ denote the number of partition quadruples of  $n$ where the odd parts in each partition are distinct. We find many arithmetic properties of
$n$ where the odd parts in each partition are distinct. We find many arithmetic properties of 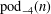 $\text{pod}_{-4}(n)$ including the following infinite family of congruences: for any integers
$\text{pod}_{-4}(n)$ including the following infinite family of congruences: for any integers 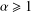 ${\it\alpha}\geq 1$ and
${\it\alpha}\geq 1$ and 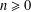 $n\geq 0$, We also establish some internal congruences and some Ramanujan-type congruences modulo 2, 5 and 8 satisfied by
$n\geq 0$, We also establish some internal congruences and some Ramanujan-type congruences modulo 2, 5 and 8 satisfied by 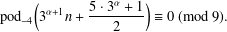 $$\begin{eqnarray}\text{pod}_{-4}\biggl(3^{{\it\alpha}+1}n+\frac{5\cdot 3^{{\it\alpha}}+1}{2}\biggr)\equiv 0~(\text{mod}~9).\end{eqnarray}$$
$$\begin{eqnarray}\text{pod}_{-4}\biggl(3^{{\it\alpha}+1}n+\frac{5\cdot 3^{{\it\alpha}}+1}{2}\biggr)\equiv 0~(\text{mod}~9).\end{eqnarray}$$ $\text{pod}_{-4}(n)$.
$\text{pod}_{-4}(n)$.