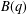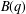Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kaur, Harman
and
Rana, Meenakshi
2022.
On second order mock theta function $ B(q) $.
Electronic Research Archive,
Vol. 30,
Issue. 1,
p.
52.
Baruah, Nayandeep Deka
and
Das, Hirakjyoti
2023.
Congruences for the coefficients of a pair of third and sixth order mock theta functions.
The Ramanujan Journal,
Vol. 61,
Issue. 4,
p.
1269.
Hu, Yueya
Liu, Eric H.
and
Yao, Olivia X. M.
2025.
Congruences modulo 4 and 8 for Ramanujan’s sixth-order mock theta function $$\rho (q)$$.
The Ramanujan Journal,
Vol. 66,
Issue. 4,
Das, Hirakjyoti
2025.
Congruences between the coefficients of certain mock theta functions.
Journal of Mathematical Analysis and Applications,
Vol. 543,
Issue. 2,
p.
128913.