Published online by Cambridge University Press: 03 June 2024
An integer partition of a positive integer n is called t-core if none of its hook lengths is divisible by t. Gireesh et al. [‘A new analogue of t-core partitions’, Acta Arith. 199 (2021), 33–53] introduced an analogue 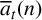 $\overline {a}_t(n)$ of the t-core partition function. They obtained multiplicative formulae and arithmetic identities for
$\overline {a}_t(n)$ of the t-core partition function. They obtained multiplicative formulae and arithmetic identities for 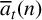 $\overline {a}_t(n)$ where
$\overline {a}_t(n)$ where 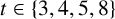 $t \in \{3,4,5,8\}$ and studied the arithmetic density of
$t \in \{3,4,5,8\}$ and studied the arithmetic density of 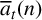 $\overline {a}_t(n)$ modulo
$\overline {a}_t(n)$ modulo 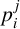 $p_i^{\,j}$ where
$p_i^{\,j}$ where 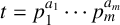 $t=p_1^{a_1}\cdots p_m^{a_m}$ and
$t=p_1^{a_1}\cdots p_m^{a_m}$ and 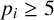 $p_i\geq 5$ are primes. Bandyopadhyay and Baruah [‘Arithmetic identities for some analogs of the 5-core partition function’, J. Integer Seq. 27 (2024), Article no. 24.4.5] proved new arithmetic identities satisfied by
$p_i\geq 5$ are primes. Bandyopadhyay and Baruah [‘Arithmetic identities for some analogs of the 5-core partition function’, J. Integer Seq. 27 (2024), Article no. 24.4.5] proved new arithmetic identities satisfied by 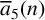 $\overline {a}_5(n)$. We study the arithmetic densities of
$\overline {a}_5(n)$. We study the arithmetic densities of 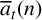 $\overline {a}_t(n)$ modulo arbitrary powers of 2 and 3 for
$\overline {a}_t(n)$ modulo arbitrary powers of 2 and 3 for 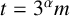 $t=3^\alpha m$ where
$t=3^\alpha m$ where 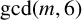 $\gcd (m,6)$=1. Also, employing a result of Ono and Taguchi [‘2-adic properties of certain modular forms and their applications to arithmetic functions’, Int. J. Number Theory 1 (2005), 75–101] on the nilpotency of Hecke operators, we prove an infinite family of congruences for
$\gcd (m,6)$=1. Also, employing a result of Ono and Taguchi [‘2-adic properties of certain modular forms and their applications to arithmetic functions’, Int. J. Number Theory 1 (2005), 75–101] on the nilpotency of Hecke operators, we prove an infinite family of congruences for 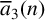 $\overline {a}_3(n)$ modulo arbitrary powers of 2.
$\overline {a}_3(n)$ modulo arbitrary powers of 2.
The author was partially supported by the Council of Scientific and Industrial Research (CSIR), Government of India, under the CSIR-JRF scheme (Grant No. 09/0796(12991)/2021-EMR-I).