Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T02:45:46.083Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation of entire functions over Carathéodory domains

Published online by Cambridge University Press:  17 April 2009

G.P. Kapoor  and
A. Nautiyal
G.P. Kapoor
Affiliation:
Department of Mathematics, Indian Institute of Technology, Kanpur 208016, India.
A. Nautiyal
Affiliation:
Department of Mathematics, Indian Institute of Technology, Kanpur 208016, India.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let D be a domain bounded by a Jordan curve. For 1 ≤ p ≤ ∞, let Lp(D) be the class of all functions f holomorphic in D such that 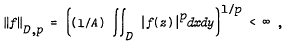where A is the area of D. For f ∈Lp(D), set

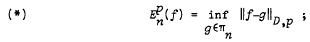
πn consists of all polynomials of degree at most n. Recently, Andre Giroux (J. Approx. Theory 28 (1980), 45–53) has obtained necessary and sufficient conditions, in terms of the rate of decrease of the approximation error 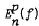, such that 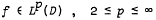has an analytic continuation as an entire function having finite order and finite type. In the present paper we have considered the approximation error (*) on a Carathéodory domain and have extended the results of Giroux for the case 1 ≤ p < 2.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 25 , Issue 2 , April 1982 , pp. 221 - 229
Copyright
Copyright © Australian Mathematical Society 1982

References

[1]Bernstein, Serge, Leoons sur les propriétés extrémales et la meilleure approximation des fonctions analytiques d'une variable réelle (Gauthier-Villars, Paris, 1926).Google Scholar
[2]Boas, Ralph Philip Jr, Entire functions (Pure and Applied Mathematics, 5. Academic Press, New York, 1954).Google Scholar
[3]Giroux, André, “Approximation of entire functions over bounded domains”, J. Approx. Theory 28 (1980), 45–53.CrossRefGoogle Scholar
[4]Kapoor, G.P. and Nautiyal, A., “Polynomial approximation of an entire function of slow growth”, J. Approx. Theory 32 (1981), 64–75.CrossRefGoogle Scholar
[5]Lorentz, G.G., Approximation of functions (Holt, Rinehart and Winston, New York, Chicago, London, 1966).Google Scholar
[6]Markushevich, A.I., Theory of functions of a complex variable. Vol. III, revised English edition (translated and edited by Silverman, Richard A.. Prentice-Hall Englewood Cliffs, New Jersey, 1967).Google Scholar
[7]Reddy, A.R., “A contribution to best approximation in L 2 norm”, J. Approx. Theory 11 (1974), 110–117.CrossRefGoogle Scholar
[8]Shah, S.M., “Polynomial approximation of an entire function and generalized orders”, J. Approx. Theory 19 (1977), 315–324.CrossRefGoogle Scholar
[9]Smirnov, V.I. and Lebedev, N.A., Functions of a complex variable: constructive theory (translated by Technica, Scripta. MIT Press, Cambridge, Massachusetts, 1968).Google Scholar
[10]Varga, Richard S., “On an extension of a result of S.N. Bernstein”, J. Approx. Theory 1 (1968), 176–179.CrossRefGoogle Scholar
[11]Winiarski, T., “Approximation and interpolation of entire functions”, Ann. Polon. Math. 23 (1970), 259–273.CrossRefGoogle Scholar