Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T13:08:04.260Z Has data issue: false hasContentIssue false
  • English
  • Français

APPROXIMATELY ANGLE PRESERVING MAPPINGS

Part of: Special classes of linear operators Linear spaces and algebras of operators Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  14 February 2019

MOHAMMAD SAL MOSLEHIAN Open the ORCID record for MOHAMMAD SAL MOSLEHIAN [Opens in a new window] ,
ALI ZAMANI Open the ORCID record for ALI ZAMANI [Opens in a new window]  and
PAWEŁ WÓJCIK Open the ORCID record for PAWEŁ WÓJCIK [Opens in a new window]
MOHAMMAD SAL MOSLEHIAN*
Affiliation:
Department of Pure Mathematics, Ferdowsi University of Mashhad, PO Box 1159, Mashhad 91775, Iran email [email protected]
ALI ZAMANI
Affiliation:
Department of Mathematics, Farhangian University, Tehran, Iran email [email protected]
PAWEŁ WÓJCIK
Affiliation:
Institute of Mathematics, Pedagogical University of Cracow, Podchora̧żych 2, 30-084 Kraków, Poland email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study linear mappings which preserve vectors at a specific angle. We introduce the concept of 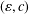$(\unicode[STIX]{x1D700},c)$-angle preserving mappings and define 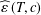$\widehat{\unicode[STIX]{x1D700}}\,(T,c)$ as the ‘smallest’ number $\unicode[STIX]{x1D700}$ for which 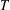$T$ is an 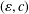$(\unicode[STIX]{x1D700},c)$-angle preserving mapping. We derive an exact formula for 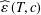$\widehat{\unicode[STIX]{x1D700}}\,(T,c)$ in terms of the norm 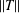$\Vert T\Vert$ and the minimum modulus 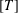$[T]$ of 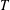$T$. Finally, we characterise approximately angle preserving mappings.

Keywords

orthogonality preserving mappingapproximately angle preserving mappingisometryapproximate similarity

MSC classification

Primary: 47B49: Transformers, preservers (operators on spaces of operators)
Secondary: 46C05: Hilbert and pre-Hilbert spaces 47L05: Linear spaces of operators 39B82: Stability, separation, extension, and related topics
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 3 , June 2019 , pp. 485 - 496
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author is partially supported by a grant from Ferdowsi University of Mashhad (No. 2/47884).

References

Chen, C. and Lu, F., ‘Linear maps preserving orthogonality’, Ann. Funct. Anal. 6(4) (2015), 70–76.Google Scholar
Chmieliński, J., ‘Linear mappings approximately preserving orthogonality’, J. Math. Anal. Appl. 304(1) (2005), 158–169.Google Scholar
Chmieliński, J., ‘Stability of angle-preserving mappings on the plane’, Math. Inequal. Appl. 8(3) (2005), 497–503.Google Scholar
Chmieliński, J., Łukasik, R. and Wójcik, P., ‘On the stability of the orthogonality equation and the orthogonality-preserving property with two unknown functions’, Banach J. Math. Anal. 10(4) (2016), 828–847.Google Scholar
Koldobsky, D., ‘Operators preserving orthogonality are isometries’, Proc. Roy. Soc. Edinburgh Sect. A 123(5) (1993), 835–837.Google Scholar
Kuźminykh, A. V., ‘Maps which almost preserve angles’, Sib. Math. J. 29(4) (1988), 593–598.Google Scholar
Turnšek, A., ‘On mappings approximately preserving orthogonality’, J. Math. Anal. Appl. 336(1) (2007), 625–631.Google Scholar
Wójcik, P., Operators Preserving and Approximately Preserving Orthogonality and Similar Relations, Doctoral Dissertation, Katowice, 2013 (in Polish).Google Scholar
Wójcik, P., ‘On mappings approximately transferring relations in finite-dimensional normed spaces’, Linear Algebra Appl. 460 (2014), 125–135.Google Scholar
Wójcik, P., ‘On certain basis connected with operator and its applications’, J. Math. Anal. Appl. 423(2) (2015), 1320–1329.Google Scholar
Wójcik, P., ‘Orthogonality of compact operators’, Expo. Math. 35 (2017), 86–94.Google Scholar
Zamani, A., Moslehian, M. S. and Frank, M., ‘Angle preserving mappings’, Z. Anal. Anwend. 34 (2015), 485–500.Google Scholar
Zhang, Y., Chen, Y., Hadwin, D. and Kong, L., ‘AOP mappings and the distance to the scalar multiples of isometries’, J. Math. Anal. Appl. 431(2) (2015), 1275–1284.Google Scholar