Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T07:19:05.981Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic iterations on Riemann surfaces

Published online by Cambridge University Press:  17 April 2009

Meira Lavie
Meira Lavie
Affiliation:
Carnegie-Mellon University, Pittsburgh, Pennsylvania
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A complex analytic family of mappings P → M(α, P) from an abstract Riemann surface (analytic manifold) into itself is studied. The mapping M(α, P) is assumed to satisfy in local coordinates the autonomous differential equation 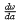= L(w), and the condition M(O, P) = P. Under certain assumptions of regularity of the reciprocal differential L in a domain D ⊂ S, we prove that for every fixed α, ∣a∣ < α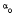, the mapping M(α, P) is conformal and one to one in D. Moreover, it is shown that the family of mappings M(α, P) satisfies the iteration equation M[a, M(b, P)] = M(a + b, P) and hence is an analytic group (analytic iteration).

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 1 , Issue 2 , August 1969 , pp. 183 - 194
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Bieberbach, Ludwig, Theorie der gewöhnlichen Differentialgleiahungen, (Springer-Verlag, Berlin, Göttingen, Heidelberg, 1965).CrossRefGoogle Scholar
[2]Erdös, Paul and Jabotinsky, Eri, “On analytic iteration”, J. Analyse. Math. 8 (1960–1961), 361–376.CrossRefGoogle Scholar
[3]Jabotinsky, Eri, “On iterational invariants”, Technion, Israel Inst. Tech. 6 (1954–1955), 64–80.Google Scholar
[4]Lavie, Meira, “Analytic iteration and differential equations”, Israel J. of Math. 5 (1967), 86–92.CrossRefGoogle Scholar
[5]Springer, George, Introduction to Riemann Surfaces, (Addison-Wesley, Reading, Mass., 1957).Google Scholar