Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Jong-Yi
Chow, Yunshyong
and
Hsieh, June
2006.
Some results on a heat conduction problem by Myshkis.
Journal of Computational and Applied Mathematics,
Vol. 190,
Issue. 1-2,
p.
190.
Chen, Jong-Yi
and
Chow, Yunshyong
2007.
A heat conduction problem with the temperature measured away from the heating point.
Journal of Difference Equations and Applications,
Vol. 13,
Issue. 5,
p.
431.
Chen, Jong-Yi
2008.
ON A DIFFERENCE EQUATION MOTIVATED BY A HEAT CONDUCTION PROBLEM.
Taiwanese Journal of Mathematics,
Vol. 12,
Issue. 8,
Chen, Jong-Yi
and
Chow, Yunshyong
2013.
On the convergence rate of a recursively defined sequence.
Mathematical Notes,
Vol. 93,
Issue. 1-2,
p.
238.
Джун-И Чэнь
Jong-Yi Chen
Юншионг Чжоу
and
Yunshyong Chow
2013.
О скорости сходимости рекурсивно определенной последовательности.
Математические заметки,
Vol. 93,
Issue. 2,
p.
195.
Chen, Jong-Yi
and
Chow, Yunshyong
2016.
A Heat Conduction Problem on Some Semi-infinite
Regions.
Taiwanese Journal of Mathematics,
Vol. 20,
Issue. 2,


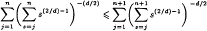 holds for
holds for