Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-22T14:52:02.517Z Has data issue: false hasContentIssue false
  • English
  • Français

An index of P. Hall for varieties of groups

Published online by Cambridge University Press:  17 April 2009

L.F. Harris
L.F. Harris
Affiliation:
Department of Mathematics, Institute of Advanced Studies, Australian National University, Canberra, ACT.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

P. Hall defined the k–index of a variety 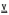, of groups to be the least cardinal number r such that if a group G is generated by a set S and every subset of S of cardinality at most r generates a group in 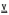then G ∈ 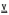. We show that the only variety which has finite k–index and contains a product of two non-trivial varieties is the variety of all groups. As a consequence of this and P. Hall's result that nilpotent varieties have finite k–index we show that a soluble variety or a variety generated by a finite group has finite k–index if and only if it is nilpotent.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 6 , Issue 3 , June 1972 , pp. 399 - 405
Copyright
Copyright © Australian Mathematical Society 1972

References

[1]Bachmuth, Seymour, Mochizuki, Horace Y., and Walkup, David, “A nonsolvable group of exponent 5”, Bull. Amer. Math. Soc. 76 (1970), 638–640.CrossRefGoogle Scholar
[2]Groves, J.R.J., “Varieties of soluble groups and a dichotomy of P. Hall”, Bull. Austral. Math. Soc. 5 (1971), 391–410.CrossRefGoogle Scholar
[3]Kovács, L.G. and Newman, M.F., “Just-non-Cross varieties”, Proc. Internat. Conf. Theory of Groups, Austral. Nat. Univ., Canberra, 1965, 221–223 (Gordon and Breach, New York, London, Paris, 1967).Google Scholar
[4]Kovács, L.G. and Newman, M.F., “On non-Cross varieties of groups”, J. Austral. Math. Soc. 12 (1971), 129–144.CrossRefGoogle Scholar
[5]Magnus, Wilhelm, Karrass, Abraham, Solitar, Donald, Combinatorial group theory (Interscience [John Wiley & Sons], New York, London, Sydney, 1966).Google Scholar
[6]Neumann, B.H., “Twisted wreath products of groups”, Arch. Math. 14 (1963), 1–6.CrossRefGoogle Scholar
[7]Neumann, Hanna, Varieties of groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 37. Springer-Verlag, Berlin, Heidelberg, New York, 1967).CrossRefGoogle Scholar