Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2025-01-03T18:37:14.964Z Has data issue: false hasContentIssue false
  • English
  • Français

An imbedding theorem for anisotropic Orlicz-Sobolev spaces

Published online by Cambridge University Press:  17 April 2009

G. Hardy  and
H.B. Thompson
G. Hardy
Affiliation:
Department of Mathematics, The University of Queensland, Queensland 4072, Australia
H.B. Thompson
Affiliation:
Department of Mathematics, The University of Queensland, Queensland 4072, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a convex function of m variables, let ω be a domain in ℝn, and let LG(ω) denote the vector-valued Orlicz space determined by G. We give an imbedding theorem for the space 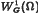of weakly differentiable functions u provided with the norm ∥(u, Du)∥G, where m = n + 1 and Du denotes the gradient of u. This theorem is a variant of an imbedding theorem by N.S. Trudinger for the completion of 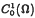in the norm ∥Du∥G, where m=n.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 51 , Issue 3 , June 1995 , pp. 463 - 467
Copyright
Copyright © Australian Mathematical Society 1995

References

[1]Donaldson, T.K. and Trudinger, N.S., ‘Orlicz-Sobolev spaces and imbedding theorems’, J. Funct. Anal. 8 (1971), 52–75.CrossRefGoogle Scholar
[2]Trudinger, N.S., ‘An imbedding theorem for H 0(G, ω) spaces’, Studio. Math. 50 (1974), 17–30.CrossRefGoogle Scholar