Published online by Cambridge University Press: 17 April 2009
Let Xi be independent and identically distributed random variables with Sn = X1 + X2 + … + Xn. We extend a classic result of Kesten, by showing that if Xiare in the domain of partial attraction of the normal distribution, there are sequences αn and B(n) for which
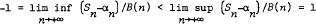
almost surely, and the almost sure limit points of (sn−αn)/b(n) coincide with the interval [−1, l]. The norming sequence B(n) is slightly different to that used by Kesten, and has properties that are less desirable. The converse to the above result is known to be true by results of Heyde and Rogozin.