Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T19:53:35.318Z Has data issue: false hasContentIssue false
  • English
  • Français

AN EQUIVARIANT DESCRIPTION OF CERTAIN HOLOMORPHIC SYMPLECTIC VARIETIES

Part of: Algebraic groups Symplectic geometry, contact geometry Topological geometry

Published online by Cambridge University Press:  20 February 2018

PETER CROOKS Open the ORCID record for PETER CROOKS [Opens in a new window]
PETER CROOKS*
Affiliation:
Institute of Differential Geometry, Gottfried Wilhelm Leibniz Universität, Hannover, Welfengarten 1, 30167 Hannover, Germany email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Varieties of the form 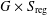$G\times S_{\!\text{reg}}$, where 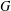$G$ is a complex semisimple group and 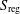$S_{\!\text{reg}}$ is a regular Slodowy slice in the Lie algebra of 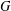$G$, arise naturally in hyperkähler geometry, theoretical physics and the theory of abstract integrable systems. Crooks and Rayan [‘Abstract integrable systems on hyperkähler manifolds arising from Slodowy slices’, Math. Res. Let., to appear] use a Hamiltonian 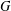$G$-action to endow 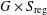$G\times S_{\!\text{reg}}$ with a canonical abstract integrable system. To understand examples of abstract integrable systems arising from Hamiltonian 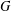$G$-actions, we consider a holomorphic symplectic variety 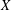$X$ carrying an abstract integrable system induced by a Hamiltonian 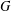$G$-action. Under certain hypotheses, we show that there must exist a 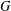$G$-equivariant variety isomorphism 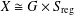$X\cong G\times S_{\!\text{reg}}$.

Keywords

equivariant geometryholomorphic symplectic geometryLie theory

MSC classification

Primary: 14L30: Group actions on varieties or schemes (quotients)
Secondary: 51H30: Geometries with algebraic manifold structure 53D20: Momentum maps; symplectic reduction
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 2 , April 2018 , pp. 207 - 214
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Audin, M., Torus Actions on Symplectic Manifolds, revised edn, Progress in Mathematics, 93 (Birkhäuser, Basel, 2004).Google Scholar
Bielawski, R., ‘Hyperkähler structures and group actions’, J. Lond. Math. Soc. (2) 55(2) (1997), 400–414.Google Scholar
Crooks, P. and Rayan, S., ‘Abstract integrable systems on hyperkähler manifolds arising from Slodowy slices’, Math. Res. Let., to appear.Google Scholar
Fernandes, R. L., Laurent-Gengoux, C. and Vanhaecke, P., ‘Global action-angle variables for non-commutative integrable systems’, J. Symplectic Geom., to appear.Google Scholar
Kobayashi, S., Differential Geometry of Complex Vector Bundles, Publications of the Mathematical Society of Japan, vol. 15, Kanô Memorial Lectures, 5 (Princeton University Press, Princeton, NJ, 1987).Google Scholar
Kostant, B., ‘Lie group representations on polynomial rings’, Amer. J. Math. 85 (1963), 327–404.Google Scholar
Luna, D., ‘Slices étales’, Mém. Soc. Math. France 33 (1973), 81–105.Google Scholar
Moore, G. W. and Tachikawa, Y., ‘On 2d TQFTs whose values are holomorphic symplectic varieties’, inString-Math 2011, Proceedings of Symposia in Pure Mathematics, 85 (American Mathematical Society, Providence, RI, 2012), 191–207.Google Scholar
Osserman, B., ‘Complex varieties and the analytic topology’.https://www.math.ucdavis.edu/∼osserman/classes/248B-W12/notes/analytic.pdf.Google Scholar
Raghunathan, M. S., ‘Principal bundles on affine space’, in: C. P. Ramanujam—a Tribute, Tata Institute of Fundamental Research Studies in Mathematics, 8 (Springer, New York, 1978), 187–206.Google Scholar
Tauvel, P. and Yu, R. W. T., Lie Algebras and Algebraic Groups, Springer Monographs in Mathematics (Springer, Berlin, 2005).Google Scholar
Wendt, M., ‘Rationally trivial torsors in A1 -homotopy theory’, J. K-Theory 7(3) (2011), 541–572.Google Scholar