Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T10:54:41.431Z Has data issue: false hasContentIssue false
  • English
  • Français

AN ANALOGUE OF EULER’S IDENTITY AND SPLIT PERFECT PARTITIONS

Part of: Additive number theory; partitions Combinatorics

Published online by Cambridge University Press:  17 December 2018

MEGHA GOYAL Open the ORCID record for MEGHA GOYAL [Opens in a new window]
MEGHA GOYAL*
Affiliation:
Department of Mathematical Sciences, IK Gujral Punjab Technical University Jalandhar, Main Campus, Kapurthala-144603, India email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give the generating function of split 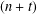$(n+t)$-colour partitions and obtain an analogue of Euler’s identity for split $n$-colour partitions. We derive a combinatorial relation between the number of restricted split $n$-colour partitions and the function 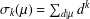$\unicode[STIX]{x1D70E}_{k}(\unicode[STIX]{x1D707})=\sum _{d|\unicode[STIX]{x1D707}}d^{k}$. We introduce a new class of split perfect partitions with 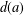$d(a)$ copies of each part $a$ and extend the work of Agarwal and Subbarao [‘Some properties of perfect partitions’, Indian J. Pure Appl. Math 22(9) (1991), 737–743].

Keywords

q-seriessplit (n + t)-colour partitionsperfect partitionsgenerating functions

MSC classification

Primary: 05A15: Exact enumeration problems, generating functions
Secondary: 05A17: Partitions of integers 11P81: Elementary theory of partitions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 3 , June 2019 , pp. 353 - 361
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Agarwal, A. K. and Andrews, G. E., ‘Rogers–Ramanujan identities for partitions with “N copies of N”’, J. Combin. Theory Ser. A 45 (1987), 40–49.Google Scholar
Agarwal, A. K. and Goyal, M., ‘New partition theoretic interpretations of Rogers–Ramanujan identities’, Int. J. Comb. 2012 (2012), Article ID 409505, 6 pages.Google Scholar
Agarwal, A. K. and Mullen, G. L., ‘Partitions with “d (a) copies of a”’, J. Combin. Theory Ser. A 46(1) (1988), 120–135.Google Scholar
Agarwal, A. K., Padmavathamma, P. V. and Subbarao, M. V., Partition Theory (Atma Ram and Sons, Chandigarh, 2005).Google Scholar
Agarwal, A. K. and Sachdeva, R., ‘Basic series identities and combinatorics’, Ramanujan J. 42(3) (2017), 725–746.Google Scholar
Agarwal, A. K. and Sood, G., ‘Split (n + t)-color partitions and Gordon–McIntosh eight order mock theta functions’, Electron. J. Combin. 21(2) (2014), Article ID P2.46, 10 pages.Google Scholar
Agarwal, A. K. and Subbarao, M. V., ‘Some properties of perfect partitions’, Indian J. Pure Appl. Math. 22(9) (1991), 737–743.Google Scholar
Andrews, G. E., The Theory of Partitions, Encyclopedia of Mathematics and its Applications, 2 (Cambridge University Press, Cambridge, 1984).Google Scholar
Connor, W. G., ‘Partition theorems related to some identities of Rogers and Watson’, Trans. Amer. Math. Soc. 214(2) (1975), 95–111.Google Scholar
Dai, L. X., Pan, H. and Tang, C. E., ‘Note on odd multiperfect numbers’, Bull. Aust. Math. Soc. 87(3) (2013), 448–451.Google Scholar
Efang, W., ‘Perfect partitions’, Chin. Ann. of Math. 7(B)(3) (1986), 267–272.Google Scholar
Göllnitz, H., ‘Partitionen mit Differenzenbedingungen’, J. reine angew. Math. 225 (1967), 154–190.Google Scholar
Gordon, B., ‘Some continued fractions of the Rogers–Ramanujan type’, Duke Math. J. 32 (1965), 741–748.Google Scholar
Gordon, B. and McIntosh, R. J., ‘Some eighth order mock theta functions’, J. Lond. Math. Soc. (2) 62(2) (2000), 321–335.Google Scholar
Goyal, M., ‘Rogers–Ramanujan type identities for split (n + t)-color partitions’, Math. Rep. (to appear).Google Scholar
Goyal, M. and Agarwal, A. K., ‘Further Rogers–Ramanujan identities for n-color partitions’, Util. Math. 95 (2014), 141–148.Google Scholar
Goyal, M. and Agarwal, A. K., ‘On a new class of combinatorial identities’, Ars Combin. 127 (2016), 65–77.Google Scholar
MacMahon, P. A., Combinatory Analysis, Vol. 2 (Cambridge University Press, London and New York, 1916).Google Scholar
Riordan, J., An Introduction to Combinatorial Analysis (John Wiley and Sons, New York, 1958).Google Scholar
Sood, G. and Agarwal, A. K., ‘Rogers–Ramanujan identities for split (n + t)-color partitions’, J. Comb. Number Theory 7(2) (2015), 141–151.Google Scholar