Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-18T06:23:02.071Z Has data issue: false hasContentIssue false
  • English
  • Français

ALMOST AUTOMORPHIC SOLUTIONS FOR DIFFERENTIAL EQUATIONS WITH PIECEWISE CONSTANT ARGUMENT

Part of: Abstract harmonic analysis Functional-differential and differential-difference equations

Published online by Cambridge University Press:  26 November 2013

LI-LI ZHANG  and
HONG-XU LI
LI-LI ZHANG*
Affiliation:
Department of Mathematics and Physics, Shijiazhuang Tiedao University, Shijiazhuang, Hebei 050043, PR China
HONG-XU LI
Affiliation:
Department of Mathematics, Sichuan University, Chengdu, Sichuan 610064, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Using the method of exponential dichotomies, we establish a new existence and uniqueness theorem for almost automorphic solutions of differential equations with piecewise constant argument of the form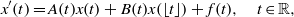

$$\begin{eqnarray*}{x}^{\prime } (t)= A(t)x(t)+ B(t)x(\lfloor t\rfloor )+ f(t), \quad t\in \mathbb{R} ,\end{eqnarray*}$$
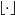where $\lfloor \cdot \rfloor $ denotes the greatest integer function, and 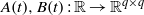$A(t), B(t): \mathbb{R} \rightarrow { \mathbb{R} }^{q\times q} $, 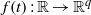$f(t): \mathbb{R} \rightarrow { \mathbb{R} }^{q} $ are all almost automorphic.

Keywords

exponential dichotomyalmost automorphic functionalmost automorphic sequencepiecewise constant argument

MSC classification

Secondary: 43A60: Almost periodic functions on groups and semigroups and their generalizations (recurrent functions, distal functions, etc.); almost automorphic functions 34K34: Hybrid systems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 1 , August 2014 , pp. 99 - 112
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Ait Dads, E. and Lhachimi, L., ‘Pseudo almost periodic solutions for equation with piecewise constant argument’, J. Math. Anal. Appl. 371 (2010), 842–854.CrossRefGoogle Scholar
Bochner, S., ‘A new approach to almost-periodicity’, Proc. Nat. Acad. Sci. USA 48 (1962), 2039–2043.CrossRefGoogle ScholarPubMed
Busenberg, S. and Cooke, K. L., ‘Models of vertically transmitted diseases with sequential-continuous dynamics’, in: Nonlinear Phenomena in Mathematical Sciences, (ed. Lakshmikantham, V.) (Academic Press, New York, 1982), 179–187.CrossRefGoogle Scholar
Cooke, K. L. and Wiener, J., ‘Retarded differential equations with piecewise constant delays’, J. Math. Anal. Appl. 99 (1984), 265–297.CrossRefGoogle Scholar
Cuevas, C. and Lizama, C., ‘Almost automorphic solutions to a class of semilinear fractional differential equations’, Appl. Math. Lett. 21 (2008), 1315–1319.CrossRefGoogle Scholar
Diagana, T., ‘Existence of globally attracting almost automorphic solutions to some nonautonomous higher-order difference equations’, Appl. Math. Comput. 219 (2013), 6510–6519.Google Scholar
Dimbour, W., ‘Almost automorphic solutions for differential equations with piecewise constant argument in a Banach space’, Nonlinear Anal. 74 (2011), 2351–2357.CrossRefGoogle Scholar
N’Guérékata, G. M., Almost Automorphy and Almost Periodic Functions in Abstract Spaces (Kluwer Academic/Plenum Publishers, New York, 2001).CrossRefGoogle Scholar
Hino, Y. and Murakami, S., ‘Almost automorphic solutions for abstract functional differential equations’, J. Math. Anal. Appl. 286 (2003), 741–752.CrossRefGoogle Scholar
Küpper, T. and Yuan, R., ‘On quasiperiodic solutions of differential equations with piecewise constant argument’, J. Math. Anal. Appl. 267 (2002), 173–193.CrossRefGoogle Scholar
Li, H. X., ‘Pseudo almost periodic sequences and some nonlinear differential equations with piecewise constant argument’, Nonlinear Funct. Anal. Appl. 10 (2005), 479–493.Google Scholar
Minh, N. V. and Dat, T. T., ‘On the almost automorphy of bounded solutions of differential equations with piecewise constant argument’, J. Math. Anal. Appl. 326 (2007), 165–178.Google Scholar
Minh, N. V., Naito, T. and N’Guérékata, G. M., ‘A spectral countability condition for almost automorphy of solutions of abstract differential equations’, Proc. Amer. Math. Soc. 134 (2006), 3257–3266.CrossRefGoogle Scholar
Palmer, K. J., ‘Exponential dichotomies, the shadowing lemma and transversal homoclinic points’, Dynam. Report. 1 (1988), 265–306.CrossRefGoogle Scholar
Shah, S. M. and Wiener, J., ‘Advanced differential equations with piecewise constant argument deviations’, Internat. J. Math. Soc. 6 (1983), 671–703.CrossRefGoogle Scholar
Yuan, R. and Hong, J. L., ‘The existence of almost periodic solutions for a class of differential equations with piecewise constant argument’, Nonlinear Anal. 28 (1997), 1439–1450.Google Scholar
Yuan, R., ‘On Favard’s theorems’, J. Differential Equations 249 (2010), 1884–1916.CrossRefGoogle Scholar
Zhang, L. L. and Li, H. X., ‘Weighted pseudo-almost periodic solutions for some abstract differential equations with uniform continuity’, Bull. Aust. Math. Soc. 82 (2010), 424–436.CrossRefGoogle Scholar
Zhang, L. L. and Li, H. X., ‘Weighted pseudo almost periodic solutions of second-order neutral-delay differential equations with piecewise constant argument’, Comput. Math. Appl. 62 (2011), 4362–4376.Google Scholar