Hostname: page-component-6587cd75c8-vj8bv Total loading time: 0 Render date: 2025-04-23T19:02:29.308Z Has data issue: false hasContentIssue false
  • English
  • Français

ALMOST ABELIAN NUMBERS

Part of: Representation theory of groups

Published online by Cambridge University Press:  20 December 2024

IUILA-CĂTĂLINA PLEŞCA Open the ORCID record for IUILA-CĂTĂLINA PLEŞCA [Opens in a new window]  and
MARIUS TĂRNĂUCEANU Open the ORCID record for MARIUS TĂRNĂUCEANU [Opens in a new window]
IUILA-CĂTĂLINA PLEŞCA*
Affiliation:
Faculty of Mathematics, ‘Al. I. Cuza’ University of Iaşi, Iaşi, Romania
MARIUS TĂRNĂUCEANU
Affiliation:
Faculty of Mathematics, ‘Al. I. Cuza’ University of Iaşi, Iaşi, Romania e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce the concept of almost $\mathcal {P}$-numbers where 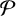$\mathcal {P}$ is a class of groups. We survey the existing results in the literature for almost cyclic numbers, and give characterisations for almost abelian and almost nilpotent numbers proving these two concepts are equivalent.

Keywords

finite groupsnilpotent groupsabelian groups

MSC classification

Primary: 20D05: Finite simple groups and their classification
Secondary: 20D40: Products of subgroups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 6
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Binjedaen, H. I., ‘When there is a unique group of a given order and related results’, Graduate Thesis, Missouri State University, 2016. https://bearworks.missouristate.edu/theses/2952/.Google Scholar
Campedel, E., Caranti, A. and Del Corso, I., ‘The automorphism groups of groups of order ${p}^2q$ ’, Int. J. Group Theory 10(3) (2021), 149–157.Google Scholar
Isaacs, I. M., Finite Group Theory (American Mathematical Society, Providence, RI, 2008).Google Scholar
Pakianathan, J. and Shankar, K., ‘Nilpotent numbers’, Amer. Math. Monthly 107(7) (2000), 631–634.CrossRefGoogle Scholar