A lattice walk with all steps having the same length 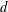$d$ is called a 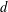$d$-walk. Denote by 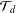${\mathcal{T}}_{d}$ the terminal set, that is, the set of all lattice points that can be reached from the origin by means of a 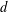$d$-walk. We examine some geometric and algebraic properties of the terminal set. After observing that 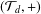$({\mathcal{T}}_{d},+)$ is a normal subgroup of the group 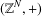$(\mathbb{Z}^{N},+)$, we ask questions about the quotient group 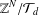$\mathbb{Z}^{N}/{\mathcal{T}}_{d}$ and give the number of elements of 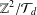$\mathbb{Z}^{2}/{\mathcal{T}}_{d}$ in terms of 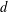$d$. To establish this result, we use several consequences of Fermat’s theorem about representations of prime numbers of the form 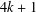$4k+1$ as the sum of two squares. One of the consequences is the fact, observed by Sierpiński, that every natural power of such a prime number has exactly one relatively prime representation. We provide explicit formulas for the relatively prime integers in this representation.