No CrossRef data available.
Published online by Cambridge University Press: 23 November 2022
Open conjectures state that, for every 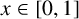 $x\in [0,1]$, the orbit
$x\in [0,1]$, the orbit 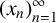 $(x_n)_{n=1}^\infty $ of the mean-median recursion
$(x_n)_{n=1}^\infty $ of the mean-median recursion 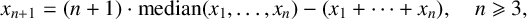 $$ \begin{align*}x_{n+1}=(n+1)\cdot\operatorname{\mathrm{median}}(x_1,\ldots,x_{n})-(x_1+\cdots+x_n),\quad n\geqslant 3,\end{align*} $$
$$ \begin{align*}x_{n+1}=(n+1)\cdot\operatorname{\mathrm{median}}(x_1,\ldots,x_{n})-(x_1+\cdots+x_n),\quad n\geqslant 3,\end{align*} $$
with initial data 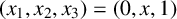 $(x_1,x_2,x_3)=(0,x,1)$, is eventually constant, and that its transit time and limit functions (of x) are unbounded and continuous, respectively. In this paper, we prove that for the slightly modified recursion
$(x_1,x_2,x_3)=(0,x,1)$, is eventually constant, and that its transit time and limit functions (of x) are unbounded and continuous, respectively. In this paper, we prove that for the slightly modified recursion  $$ \begin{align*}x_{n+1}=n\cdot\operatorname{\mathrm{median}}(x_1,\ldots,x_{n})-(x_1+\cdots+x_n),\quad n\geqslant 3,\end{align*} $$
$$ \begin{align*}x_{n+1}=n\cdot\operatorname{\mathrm{median}}(x_1,\ldots,x_{n})-(x_1+\cdots+x_n),\quad n\geqslant 3,\end{align*} $$
first suggested by Akiyama, the transit time function is unbounded but the limit function is discontinuous.