Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-16T14:00:47.592Z Has data issue: false hasContentIssue false
  • English
  • Français

ADDITIVE BASES AND NIVEN NUMBERS

Part of: Elementary number theory Sequences and sets

Published online by Cambridge University Press:  25 March 2021

CARLO SANNA Open the ORCID record for CARLO SANNA [Opens in a new window]
CARLO SANNA*
Affiliation:
Department of Mathematical Sciences, Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129Torino, Italy
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 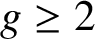$g \geq 2$ be an integer. A natural number is said to be a base-g Niven number if it is divisible by the sum of its base-g digits. Assuming Hooley’s Riemann hypothesis, we prove that the set of base-g Niven numbers is an additive basis, that is, there exists a positive integer 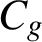$C_g$ such that every natural number is the sum of at most 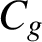$C_g$ base-g Niven numbers.

Keywords

additive basisdigitsNiven numbersum of digits

MSC classification

Primary: 11B13: Additive bases, including sumsets
Secondary: 11A63: Radix representation; digital problems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 3 , December 2021 , pp. 373 - 380
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

C. Sanna is a member of GNSAGA of INdAM and of CrypTO, the group of Cryptography and Number Theory of Politecnico di Torino.

References

Banks, W. D., ‘Every natural number is the sum of forty-nine palindromes’, Integers 16 (2016), A3.Google Scholar
Bell, J., Hare, K. and Shallit, J., ‘When is an automatic set an additive basis?’, Proc. Amer. Math. Soc. Ser. B 5 (2018), 50–63.10.1090/bproc/37CrossRefGoogle Scholar
Bell, J. P., Lidbetter, T. F. and Shallit, J., ‘Additive number theory via approximation by regular languages’, in: Developments in Language Theory, Lecture Notes in Computer Science, 11088 (Springer, Cham, 2018), 121–132.10.1007/978-3-319-98654-8_10CrossRefGoogle Scholar
Cilleruelo, J., Luca, F. and Baxter, L., ‘Every positive integer is a sum of three palindromes’, Math. Comp. 87(314) (2018), 3023–3055.10.1090/mcom/3221CrossRefGoogle Scholar
Daileda, R., Jou, J., Lemke-Oliver, R., Rossolimo, E. and Treviño, E., ‘On the counting function for the generalized Niven numbers’, J. Théor. Nombres Bordeaux 21(3) (2009), 503–515.10.5802/jtnb.685CrossRefGoogle Scholar
De Koninck, J.-M. and Doyon, N., ‘Large and small gaps between consecutive Niven numbers’, J. Integer Seq. 6(2) (2003), 03.2.5.Google Scholar
De Koninck, J.-M., Doyon, N. and Kátai, I., ‘On the counting function for the Niven numbers’, Acta Arith. 106(3) (2003), 265–275.CrossRefGoogle Scholar
De Koninck, J.-M., Doyon, N. and Kátai, I., ‘Counting the number of twin Niven numbers, Ramanujan J. 17(1) (2008), 89–105.10.1007/s11139-008-9127-zCrossRefGoogle Scholar
De Koninck, J.-M. and Luca, F., ‘Positive integers divisible by the product of their nonzero digits’, Port. Math. (N.S.) 64(1) (2007), 75–85.10.4171/PM/1777CrossRefGoogle Scholar
De Koninck, J.-M. and Luca, F., ‘Corrigendum to “Positive integers divisible by the product of their nonzero digits”’, Port. Math. 74(2) (2017), 169–170.10.4171/PM/1999CrossRefGoogle Scholar
Dias da Silva, J. A. and Hamidoune, Y. O., ‘Cyclic spaces for Grassmann derivatives and additive theory’, Bull. Lond. Math. Soc. 26(2) (1994), 140–146.CrossRefGoogle Scholar
Frei, C., Koymans, P. and Sofos, E., ‘Vinogradov’s three primes theorem with primes having given primitive roots’, Math. Proc. Cambridge Philos. Soc. 170(1) (2021), 75–110.CrossRefGoogle Scholar
Hoeffding, W., ‘Probability inequalities for sums of bounded random variables’, J. Amer. Statist. Assoc. 58 (1963), 13–30.CrossRefGoogle Scholar
Kane, D. M., Sanna, C. and Shallit, J., ‘Waring’s theorem for binary powers’, Combinatorica 39(4) (2019), 1335–1350.10.1007/s00493-019-3933-3CrossRefGoogle Scholar
Madhusudan, P., Nowotka, D., Rajasekaran, A. and Shallit, J., ‘Lagrange’s theorem for binary squares’, in: 43rd International Symposium on Mathematical Foundations of Computer Science, LIPIcs, Leibniz International Proceedings in Informatics, 117 (Schloss Dagstuhl–Leibniz-Zentrum fur Informatik, Wadern, 2018), Article ID 18, 14 pages.Google Scholar
Mauduit, C., Pomerance, C. and Sárközy, A., ‘On the distribution in residue classes of integers with a fixed sum of digits’, Ramanujan J. 9(1–2) (2005), 45–62.CrossRefGoogle Scholar
Nathanson, M. B., Additive Number Theory: The Classical Bases, Graduate Texts in Mathematics , 164 (Springer-Verlag, New York, 1996).CrossRefGoogle Scholar
Rajasekaran, A., Shallit, J. and Smith, T., ‘Additive number theory via automata theory’, Theory Comput. Syst. 64(3) (2020), 542–567.CrossRefGoogle Scholar
Sanna, C., ‘On numbers divisible by the product of their nonzero base $b$ digits’, Quaest. Math. 43(11) (2020), 1563–1571.CrossRefGoogle Scholar