Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-29T02:12:12.132Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIFORM ASYMPTOTIC FORMULAS FOR RESTRICTED BIPARTITE PARTITIONS

Part of: Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  05 February 2020

NIAN HONG ZHOU Open the ORCID record for NIAN HONG ZHOU [Opens in a new window]
NIAN HONG ZHOU*
Affiliation:
School of Mathematical Sciences, East China Normal University, Shanghai200241, PR China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we investigate 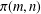$\unicode[STIX]{x1D70B}(m,n)$, the number of partitions of the bipartite number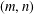$(m,n)$ into steadily decreasing parts, introduced by Carlitz [‘A problem in partitions’, Duke Math. J.30 (1963), 203–213]. We give a relation between 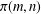$\unicode[STIX]{x1D70B}(m,n)$ and the crank statistic 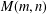$M(m,n)$ for integer partitions. Using this relation, we establish some uniform asymptotic formulas for 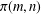$\unicode[STIX]{x1D70B}(m,n)$.

Keywords

partitionsrestricted partitionsasymptotics

MSC classification

Primary: 11P82: Analytic theory of partitions
Secondary: 05A16: Asymptotic enumeration 05A17: Partitions of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 2 , October 2020 , pp. 217 - 225
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was supported by the National Science Foundation of China (Grant No. 11971173).

References

Andrews, G. E., ‘An extension of Carlitz’s bipartition identity’, Proc. Amer. Math. Soc. 63(1) (1977), 180–184.Google Scholar
Andrews, G. E., The Theory of Partitions, Cambridge Mathematical Library (Cambridge University Press, Cambridge, 1998), reprint of the 1976 original.Google Scholar
Andrews, G. E. and Garvan, F. G., ‘Dyson’s crank of a partition’, Bull. Amer. Math. Soc. (N.S.) 18(2) (1988), 167–171.CrossRefGoogle Scholar
Bessenrodt, C., ‘On pairs of partitions with steadily decreasing parts’, J. Combin. Theory Ser. A 99(1) (2002), 162–174.CrossRefGoogle Scholar
Bringmann, K. and Dousse, J., ‘On Dyson’s crank conjecture and the uniform asymptotic behavior of certain inverse theta functions’, Trans. Amer. Math. Soc. 368(5) (2016), 3141–3155.CrossRefGoogle Scholar
Carlitz, L., ‘A problem in partitions’, Duke Math. J. 30 (1963), 203–213.CrossRefGoogle Scholar
Carlitz, L., ‘Generating functions and partition problems’, in: Theory of Numbers, Proceedings of Symposia in Pure Mathematics, VIII (American Mathematical Society, Providence, RI, 1965), 144–169.CrossRefGoogle Scholar
Carlitz, L. and Roselle, D. P., ‘Restricted bipartite partitions’, Pacific J. Math. 19 (1966), 221–228.CrossRefGoogle Scholar
Chan, H.-C., ‘Ramanujan’s cubic continued fraction and an analog of his ‘most beautiful identity’’, Int. J. Number Theory 6(3) (2010), 673–680.CrossRefGoogle Scholar
Dyson, F. J., ‘Some guesses in the theory of partitions’, Eureka 8 (1944), 10–15.Google Scholar
Dyson, F. J., ‘Mappings and symmetries of partitions’, J. Combin. Theory Ser. A 51(2) (1989), 169–180.CrossRefGoogle Scholar
Garvan, F. G., ‘New combinatorial interpretations of Ramanujan’s partition congruences mod 5, 7 and 11’, Trans. Amer. Math. Soc. 305(1) (1988), 47–77.Google Scholar
Hardy, G. H. and Ramanujan, S., ‘Asymptotic formulae in combinatory analysis’, Proc. Lond. Math. Soc. (2) 17 (1918), 75–115.CrossRefGoogle Scholar
Kim, B., Kim, E. and Nam, H., ‘On the asymptotic distribution of cranks and ranks of cubic partitions’, J. Math. Anal. Appl. 443(2) (2016), 1095–1109.CrossRefGoogle Scholar
Roselle, D. P., ‘Generalized Eulerian functions and a problem in partitions’, Duke Math. J. 33 (1966), 293–304.CrossRefGoogle Scholar
Zhou, N. H., ‘On the distribution of rank and crank statistics for integer partitions’, Res. Number Theory 5(2) (2019), Article ID 18.CrossRefGoogle Scholar
Zhou, N. H., ‘On the distribution of the rank statistic for strongly concave compositions’, Bull. Aust. Math. Soc. 100(2) (2019), 230–238.CrossRefGoogle Scholar