Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T15:57:15.979Z Has data issue: false hasContentIssue false
  • English
  • Français

TRANSLATING SOLITONS FOR THE MEAN CURVATURE FLOW IN $\boldsymbol {{\mathbb {R}}^{4}}$

Part of: Classical differential geometry

Published online by Cambridge University Press:  25 April 2022

HOJOO LEE Open the ORCID record for HOJOO LEE [Opens in a new window]
HOJOO LEE*
Affiliation:
Department of Mathematics and Institute of Pure and Applied Mathematics, Jeonbuk National University, Jeonju 54896, Korea
*
e-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a representation formula for translating soliton surfaces to the mean curvature flow in Euclidean space 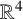${\mathbb {R}}^{4}$ and give examples of conformal parameterisations for translating soliton surfaces.

Keywords

Gauss mapmean curvature flowsolitons

MSC classification

Primary: 53A10: Minimal surfaces, surfaces with prescribed mean curvature
Secondary: 53A07: Higher-dimensional and -codimensional surfaces in Euclidean $n$-space
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 3 , December 2022 , pp. 491 - 499
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altschuler, S. J. and Wu, L. F., ‘Translating surfaces of the non-parametric mean curvature flow with prescribed contact angle’, Calc. Var. Partial Differential Equations 2(1) (1994), 101–111.CrossRefGoogle Scholar
Castro, I. and Lerma, A. M., ‘Translating solitons for Lagrangian mean curvature flow in complex Euclidean plane’, Internat. J. Math. 23(10) (2012), Article no. 1250101.CrossRefGoogle Scholar
Clutterbuck, J., Schnürer, O. C. and Schulze, F., ‘Stability of translating solutions to mean curvature flow’, Calc. Var. Partial Differential Equations 29(3) (2007), 281–293.CrossRefGoogle Scholar
Colding, T. H. and Minicozzi, W. P. II, ‘Minimal surfaces and mean curvature flow’, in: Surveys in Geometric Analysis and Relativity, Advanced Lectures in Mathematics, 20 (International Press, Somerville, MA, 2011), 73–143.Google Scholar
Halldorsson, H. P., ‘Helicoidal surfaces rotating/translating under the mean curvature flow’, Geom. Dedicata 162 (2013), 45–65.CrossRefGoogle Scholar
Hoffman, D. A. and Osserman, R., The Geometry of the Generalised Gauss Map, Memoirs of the American Mathematical Society, 28(236) (American Mathematical Society, Providence, RI, 1980).Google Scholar
Hoffman, D. A. and Osserman, R., ‘The Gauss map of surfaces in ${\mathbb{R}}^3$ and ${\mathbb{R}}^4$ ’, Proc. Lond. Math. Soc. (3) 50(3) (1985), 27–56.CrossRefGoogle Scholar
Ilmanen, T., Elliptic Regularization and Partial Regularity for Motion by Mean Curvature, Memoirs of the American Mathematical Society, 108(520) (American Mathematical Society, Providence, RI, 1994).CrossRefGoogle Scholar
Jenkins, H. and Serrin, J., ‘Variational problems of minimal surface type. II. Boundary value problems for the minimal surface equation’, Arch. Ration. Mech. Anal. 21 (1966), 321–342.CrossRefGoogle Scholar
Joyce, D., Lee, Y.-I. and Tsui, M.-P., ‘Self-similar solutions and translating solitons for Lagrangian mean curvature flow’, J. Differential Geom. 84(1) (2010), 127–161.CrossRefGoogle Scholar
Martínez, A. and Martínez-Triviño, A. L., ‘A Weierstrass type representation for translating solitons and singular minimal surfaces’, Preprint, 2022, arXiv:2201.01192.CrossRefGoogle Scholar
Nakahara, H., ‘Some examples of self-similar solutions and translating solitons for Lagrangian mean curvature flow’, Tohoku Math. J. (2) 65(3) (2013), 411–425.CrossRefGoogle Scholar
Neves, A. and Tian, G., ‘Translating solutions to Lagrangian mean curvature flow’, Trans. Amer. Math. Soc. 365(11) (2013), 5655–5680.CrossRefGoogle Scholar
Nguyen, X. H., ‘Translating tridents’, Comm. Partial Differential Equations 34(3) (2009), 257–280.CrossRefGoogle Scholar
Nguyen, X. H., ‘Complete embedded self-translating surfaces under mean curvature flow’, J. Geom. Anal. 23(3) (2013), 1379–1426.CrossRefGoogle Scholar
Smoczyk, K., ‘A relation between mean curvature flow solitons and minimal submanifolds’, Math. Nachr. 229 (2001), 175–186.3.0.CO;2-H>CrossRefGoogle Scholar
Spruck, J., ‘Infinite boundary value problems for surfaces of constant mean curvature’, Arch. Ration. Mech. Anal. 49 (1973), 1–31.CrossRefGoogle Scholar
White, B., ‘Subsequent singularities in mean-convex mean curvature flow’, Calc. Var. Partial Differential Equations 54(2) (2015), 1457–1468.CrossRefGoogle Scholar