Hostname: page-component-f554764f5-nwwvg Total loading time: 0 Render date: 2025-04-22T23:27:24.181Z Has data issue: false hasContentIssue false
  • English
  • Français

A SUFFICIENT CONDITION FOR PANCYCLIC GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  20 December 2024

XINGZHI ZHAN Open the ORCID record for XINGZHI ZHAN [Opens in a new window]
XINGZHI ZHAN*
Affiliation:
Department of Mathematics, East China Normal University, Shanghai 200241, China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A graph G is called an 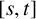$[s,t]$-graph if any induced subgraph of G of order s has size at least 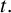$t.$ We prove that every 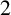$2$-connected 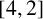$[4,2]$-graph of order at least 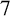$7$ is pancyclic. This strengthens existing results. There are 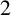$2$-connected $[4,2]$-graphs which do not satisfy the Chvátal–Erdős condition on Hamiltonicity. We also determine the triangle-free graphs among 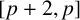$[p+2,p]$-graphs for a general 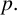$p.$

Keywords

Hamiltonian graphpancyclic graph[s, t]-graphtriangle-free

MSC classification

Primary: 05C38: Paths and cycles
Secondary: 05C42: Density (toughness, etc.) 05C45: Eulerian and Hamiltonian graphs 05C75: Structural characterization of families of graphs
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 7
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This research was supported by the NSFC grant 12271170 and Science and Technology Commission of Shanghai Municipality grant 22DZ2229014.

References

Bondy, J. A., ‘Pancyclic graphs. I’, J. Combin. Theory Ser. B 11 (1971), 80–84.CrossRefGoogle Scholar
Bondy, J. A., ‘A remark on two sufficient conditions for Hamilton cycles’, Discrete Math. 22(2) (1978), 191–193.CrossRefGoogle Scholar
Bondy, J. A. and Murty, U. S. R., Graph Theory, Graduate Texts in Mathematics, 244 (Springer, London, 2008).CrossRefGoogle Scholar
Chvátal, V. and Erdős, P., ‘A note on Hamiltonian circuits’, Discrete Math. 2 (1972), 111–113.CrossRefGoogle Scholar
George, J. C., Khodkar, A. and Wallis, W. D., Pancyclic and Bipancyclic Graphs (Springer, Cham, 2016).CrossRefGoogle Scholar
Liu, C. and Wang, J., ‘ $\left[s,t\right]$ -graphs and their hamiltonicity’, J. Shandong Normal Univ. Nat. Sci. 20(1) (2005), 6–7 (in Chinese).Google Scholar
Liu, X., Wang, J. and Gao, G., ‘Cycles in $2$ -connected $\left[4,2\right]$ -graphs’, J. Shandong Univ. Nat. Sci. 42(4) (2007), 32–35 (in Chinese).Google Scholar
West, D. B., Introduction to Graph Theory (Prentice Hall, Upper Saddle River, NJ, 1996).Google Scholar
Zhan, X., ‘Extremal numbers of positive entries of imprimitive nonnegative matrices’, Linear Algebra Appl. 424(1) (2007), 132–138.CrossRefGoogle Scholar