No CrossRef data available.
Article contents
STRICHARTZ ESTIMATES FOR THE WAVE EQUATION INSIDE CYLINDRICAL CONVEX DOMAINS
Published online by Cambridge University Press: 08 August 2022
Abstract
We establish local-in-time Strichartz estimates for solutions of the model case Dirichlet wave equation inside cylindrical convex domains
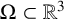 $\Omega \subset \mathbb {R}^ 3$
with smooth boundary
$\Omega \subset \mathbb {R}^ 3$
with smooth boundary
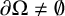 $\partial \Omega \neq \emptyset $
. The key ingredients to prove Strichartz estimates are dispersive estimates, energy estimates, interpolation and
$\partial \Omega \neq \emptyset $
. The key ingredients to prove Strichartz estimates are dispersive estimates, energy estimates, interpolation and
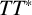 $TT^*$
arguments. Strichartz estimates for waves inside an arbitrary domain
$TT^*$
arguments. Strichartz estimates for waves inside an arbitrary domain
 $\Omega $
have been proved by Blair, Smith and Sogge [‘Strichartz estimates for the wave equation on manifolds with boundary’, Ann. Inst. H. Poincaré Anal. Non Linéaire 26 (2009), 1817–1829]. We provide a detailed proof of the usual Strichartz estimates from dispersive estimates inside cylindrical convex domains for a certain range of the wave admissibility.
$\Omega $
have been proved by Blair, Smith and Sogge [‘Strichartz estimates for the wave equation on manifolds with boundary’, Ann. Inst. H. Poincaré Anal. Non Linéaire 26 (2009), 1817–1829]. We provide a detailed proof of the usual Strichartz estimates from dispersive estimates inside cylindrical convex domains for a certain range of the wave admissibility.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.



