Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-16T17:12:31.920Z Has data issue: false hasContentIssue false
  • English
  • Français

SIMULTANEOUS DYNAMICAL DIOPHANTINE APPROXIMATION IN BETA EXPANSIONS

Part of: Classical measure theory Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  08 January 2020

WEILIANG WANG Open the ORCID record for WEILIANG WANG [Opens in a new window]  and
LU LI Open the ORCID record for LU LI [Opens in a new window]
WEILIANG WANG*
Affiliation:
School of Mathematics and Statistics, Huazhong University of Science and Technology, 430074 Wuhan, China Department of Mathematics, West Anhui University, Luan, Anhui 237012, China email [email protected]
LU LI
Affiliation:
Department of Mathematics, West Anhui University, Luan, Anhui 237012, China email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 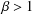$\unicode[STIX]{x1D6FD}>1$ be a real number and define the 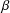$\unicode[STIX]{x1D6FD}$-transformation on 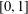$[0,1]$ by 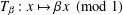$T_{\unicode[STIX]{x1D6FD}}:x\mapsto \unicode[STIX]{x1D6FD}x\hspace{0.6em}({\rm mod}\hspace{0.2em}1)$. Let 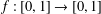$f:[0,1]\rightarrow [0,1]$ and 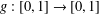$g:[0,1]\rightarrow [0,1]$ be two Lipschitz functions. The main result of the paper is the determination of the Hausdorff dimension of the set

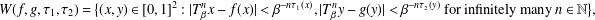$$\begin{eqnarray}W(f,g,\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2})=\big\{(x,y)\in [0,1]^{2}:|T_{\unicode[STIX]{x1D6FD}}^{n}x-f(x)|<\unicode[STIX]{x1D6FD}^{-n\unicode[STIX]{x1D70F}_{1}(x)},|T_{\unicode[STIX]{x1D6FD}}^{n}y-g(y)|<\unicode[STIX]{x1D6FD}^{-n\unicode[STIX]{x1D70F}_{2}(y)}~\text{for infinitely many}~n\in \mathbb{N}\big\},\end{eqnarray}$$
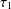where $\unicode[STIX]{x1D70F}_{1}$, 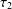$\unicode[STIX]{x1D70F}_{2}$ are two positive continuous functions with 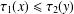$\unicode[STIX]{x1D70F}_{1}(x)\leq \unicode[STIX]{x1D70F}_{2}(y)$ for all 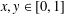$x,y\in [0,1]$.

Keywords

beta expansionsDiophantine approximationHausdorff dimension

MSC classification

Primary: 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension
Secondary: 28A80: Fractals
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 2 , October 2020 , pp. 186 - 195
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work is supported by the Provincial Natural Science Research Project of Anhui Colleges (grant KJ2019A0672).

References

Beresnevich, V., Dickinson, D. and Velani, S., ‘Measure theoretic laws for lim sup sets’, Mem. Amer. Math. Soc. 179(846) (2006), 91 pages.Google Scholar
Beresnevich, V., Ramrez, F. and Velani, S., ‘Metric Diophantine approximation: aspects of recent work’, in: Dynamics and Analytic Number Theory, LMS Lecture Note Series, 437 (eds. Badziahin, D., Gorodnik, A. and Peyerimhoff, N.) (Cambridge University Press, Cambridge, 2016), 1–95.Google Scholar
Bugeaud, Y., ‘A note on inhomogeneous Diophantine approximation’, Glasg. Math. J. 45(1) (2003), 105–110.CrossRefGoogle Scholar
Bugeaud, Y., Harrap, S., Kristensen, S. and Velani, S., ‘On shrinking target for ℤm actions on tori’, Mathematika 56(2) (2010), 193–202.CrossRefGoogle Scholar
Bugeaud, Y. and Wang, B., ‘Distribution of full cylinders and the Diophantine properties of the orbits in 𝛽-expansions’, J. Fractal Geom. 1 (2014), 799–827.Google Scholar
Coons, M., Hussain, M. and Wang, B., ‘A dichotomy law for the Diophantine properties in 𝛽-dynamical systems’, Mathematika 62(3) (2016), 884–897.CrossRefGoogle Scholar
Hill, R. and Velani, S., ‘The ergodic theory of shrinking targets’, Invent. Math. 119 (1995), 175–198.CrossRefGoogle Scholar
Hussain, M. and Wang, W., ‘Two-dimensional shrinking target problem in beta-dynamical systems’, Bull. Aust. Math. Soc. 97(1) (2018), 33–42.CrossRefGoogle Scholar
Hussain, M. and Yusupova, T., ‘A note on the weighted Khintchine–Groshev theorem’, J. Théor. Nombres Bordeaux 26(2) (2014), 385–397.CrossRefGoogle Scholar
Parry, W., ‘On the 𝛽-expansions of real numbers’, Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.CrossRefGoogle Scholar
Rényi, A., ‘Representations for real numbers and their ergodic properties’, Acta Math. Acad. Sci. Hungar. 8 (1957), 477–493.CrossRefGoogle Scholar
Seuret, S. and Wang, B., ‘Quantitative recurrence properties in conformal iterated function systems’, Adv. Math. 280 (2015), 472–505.CrossRefGoogle Scholar
Shen, L. and Wang, B., ‘Shrinking target problems for beta-dynamical system’, Sci. China Math. 56 (2013), 91–104.CrossRefGoogle Scholar
Tan, B. and Wang, B., ‘Quantitative recurrence properties of beta dynamical systems’, Adv. Math. 228 (2011), 2071–2097.CrossRefGoogle Scholar
Tseng, J., ‘On circle rotations and the shrinking target properties’, Discrete Contin. Dyn. Syst. 20(4) (2008), 1111–1122.CrossRefGoogle Scholar
Wang, B., Wu, J. and Xu, J., ‘Mass transference principle for lim sup sets generated by rectangles’, Math. Proc. Cambridge Philos. Soc. 158 (2015), 419–437.CrossRefGoogle Scholar
Wang, W., ‘Modified shrinking target problem in beta dynamical systems’, J. Math. Anal. Appl. 468(1) (2018), 423–435.CrossRefGoogle Scholar