Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T11:11:38.281Z Has data issue: false hasContentIssue false
  • English
  • Français

PROOF OF TWO CONJECTURES ON SUPERCONGRUENCES INVOLVING CENTRAL BINOMIAL COEFFICIENTS

Part of: Elementary number theory Sequences and sets

Published online by Cambridge University Press:  13 February 2020

CHENG-YANG GU Open the ORCID record for CHENG-YANG GU [Opens in a new window]  and
VICTOR J. W. GUO Open the ORCID record for VICTOR J. W. GUO [Opens in a new window]
CHENG-YANG GU
Affiliation:
School of Mathematics and Statistics, Huaiyin Normal University, Huai’an 223300, Jiangsu, PR China email [email protected]
VICTOR J. W. GUO*
Affiliation:
School of Mathematics and Statistics, Huaiyin Normal University, Huai’an223300, Jiangsu, PR China email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note we use some 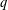$q$-congruences proved by the method of ‘creative microscoping’ to prove two conjectures on supercongruences involving central binomial coefficients. In particular, we confirm the 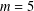$m=5$ case of Conjecture 1.1 of Guo [‘Some generalizations of a supercongruence of Van Hamme’, Integral Transforms Spec. Funct.28 (2017), 888–899].

Keywords

q-congruencessupercongruencescyclotomic polynomial

MSC classification

Primary: 11A07: Congruences; primitive roots; residue systems
Secondary: 11B65: Binomial coefficients; factorials; $q$-identities
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 3 , December 2020 , pp. 360 - 364
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author was partially supported by the National Natural Science Foundation of China (Grant No. 11771175).

References

Gu, C.-Y. and Guo, V. J. W., ‘q-Analogues of two supercongruences of Z.-W. Sun’, Czechoslovak Math. J. to appear.Google Scholar
Guo, V. J. W., ‘Some generalizations of a supercongruence of van Hamme’, Integral Transforms Spec. Funct. 28 (2017), 888–899.CrossRefGoogle Scholar
Guo, V. J. W., ‘Common q-analogues of some different supercongruences’, Results Math. 74 (2019), Article ID 131.CrossRefGoogle Scholar
Guo, V. J. W. and Liu, J.-C., ‘Some congruences related to a congruence of Van Hamme’, Integral Transforms Spec. Funct. to appear.Google Scholar
Guo, V. J. W. and Schlosser, M. J., ‘Some new q-congruences for truncated basic hypergeometric series: even powers’, Results Math. 75 (2020), Article ID 1.CrossRefGoogle ScholarPubMed
Guo, V. J. W. and Zudilin, W., ‘A q-microscope for supercongruences’, Adv. Math. 346 (2019), 329–358.CrossRefGoogle Scholar
Hou, Q.-H., Mu, Y.-P. and Zeilberger, D., ‘Polynomial reduction and supercongruences’, J. Symbolic Comput. to appear.Google Scholar
Liu, J.-C., ‘Semi-automated proof of supercongruences on partial sums of hypergeometric series’, J. Symbolic Comput. 93 (2019), 221–229.CrossRefGoogle Scholar
Mortenson, E., ‘A p-adic supercongruence conjecture of van Hamme’, Proc. Amer. Math. Soc. 136 (2008), 4321–4328.CrossRefGoogle Scholar
Straub, A., ‘Supercongruences for polynomial analogs of the Apéry numbers’, Proc. Amer. Math. Soc. 147 (2019), 1023–1036.CrossRefGoogle Scholar
Sun, Z.-W., ‘A refinement of a congruence result by van Hamme and Mortenson’, Illinois J. Math. 56 (2012), 967–979.CrossRefGoogle Scholar
Swisher, H., ‘On the supercongruence conjectures of van Hamme’, Res. Math. Sci. 2 (2015), Article ID 18.CrossRefGoogle Scholar
Van Hamme, L., ‘Some conjectures concerning partial sums of generalized hypergeometric series’, in: p-Adic Functional Analysis (Nijmegen, 1996), Lecture Notes in Pure and Applied Mathematics, 192 (Dekker, New York, 1997), 223–236.Google Scholar
Zudilin, W., ‘Ramanujan-type supercongruences’, J. Number Theory 129 (2009), 1848–1857.CrossRefGoogle Scholar