Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T01:59:20.940Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE DIVISOR FUNCTION OVER NONHOMOGENEOUS BEATTY SEQUENCES

Part of: Exponential sums and character sums Sequences and sets

Published online by Cambridge University Press:  04 March 2022

WEI ZHANG Open the ORCID record for WEI ZHANG [Opens in a new window]
WEI ZHANG*
Affiliation:
School of Mathematics and Statistics, Henan University, Kaifeng 475004, Henan, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider sums involving the divisor function over nonhomogeneous ( 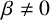$\beta \neq 0$ ) Beatty sequences 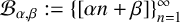$ \mathcal {B}_{\alpha ,\beta }:=\{[\alpha n+\beta ]\}_{n=1}^{\infty } $ and show that

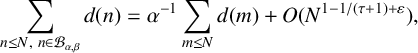$$ \begin{align*} \sum_{n\leq N,\ n\in\mathcal{B}_{\alpha,\beta}}d(n) =\alpha^{-1}\sum_{m\leq N}d(m) +O(N^{1-1/(\tau+1)+\varepsilon}), \end{align*} $$

where N is a sufficiently large integer, 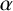$\alpha $ is of finite type 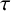$\tau $ and 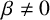$\beta \neq 0$ . Previously, such estimates were only obtained for homogeneous Beatty sequences or for almost all 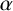$\alpha $ .

Keywords

exponential sumsBeatty sequencesdivisor problems

MSC classification

Primary: 11L20: Sums over primes
Secondary: 11L07: Estimates on exponential sums 11B83: Special sequences and polynomials
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 2 , October 2022 , pp. 280 - 287
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abercrombie, A. G., ‘Beatty sequences and multiplicative number theory’, Acta Arith. 70 (1995), 195–207.CrossRefGoogle Scholar
Abercrombie, A. G., Banks, W. D. and Shparlinski, I. E., ‘Arithmetic functions on Beatty sequences’, Acta Arith. 136 (2009), 81–89.CrossRefGoogle Scholar
Banks, W. D. and Shparlinski, I. E., ‘Short character sums with Beatty sequences’, Math. Res. Lett. 13 (2006), 539–547.CrossRefGoogle Scholar
Chowla, S., ‘Some problems of Diophantine approximation I’, Math. Z. 33 (1931), 544–563.CrossRefGoogle Scholar
Erdős, P., ‘Some remarks on Diophantine approximations’, J. Indian Math. Soc. (N.S.) 12 (1948), 67–74.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, AMS Colloquium Publications, 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Khinchin, A. Y., ‘Zur metrischen Theorie der diophantischen Approximationen’, Math. Z. 24 (1926), 706–714.CrossRefGoogle Scholar
Kuipers, L. and Niederreiter, H., Uniform Distribution of Sequences (Wiley-Interscience, New York–London–Sydney, 1974).Google Scholar
Lü, G. S. and Zhai, W. G., ‘The divisor problem for the Beatty sequences’, Acta Math. Sinica (Chin. Ser.) 47 (2004), 1213–1216.Google Scholar
Roth, K. F., ‘Rational approximations to algebraic numbers’, Mathematika 2 (1955), 1–20.CrossRefGoogle Scholar
Technau, M. and Zafeiropoulos, A., ‘Metric results on summatory arithmetic functions on Beatty sets’, Acta Arith. 197 (2021), 93–104.CrossRefGoogle Scholar
Vaughan, R. C., ‘On the distribution of $\mathrm{\alpha} {p}$ modulo 1’, Mathematika 24 (1977), 135–141.CrossRefGoogle Scholar
Vinogradov, I. M., The Method of Trigonometrical Sums in the Theory of Numbers (Dover, New York, 2004).Google Scholar
Zhai, W. G., ‘Note on a result of Abercrombie’, Chinese Sci. Bull. 42 (1997), 804–806.Google Scholar