No CrossRef data available.
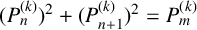 $(P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m$
$(P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m$Published online by Cambridge University Press: 06 March 2024
A generalisation of the well-known Pell sequence 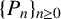 $\{P_n\}_{n\ge 0}$ given by
$\{P_n\}_{n\ge 0}$ given by 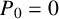 $P_0=0$,
$P_0=0$, 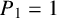 $P_1=1$ and
$P_1=1$ and 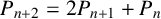 $P_{n+2}=2P_{n+1}+P_n$ for all
$P_{n+2}=2P_{n+1}+P_n$ for all 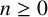 $n\ge 0$ is the k-generalised Pell sequence
$n\ge 0$ is the k-generalised Pell sequence 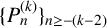 $\{P^{(k)}_n\}_{n\ge -(k-2)}$ whose first k terms are
$\{P^{(k)}_n\}_{n\ge -(k-2)}$ whose first k terms are 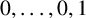 $0,\ldots ,0,1$ and each term afterwards is given by the linear recurrence
$0,\ldots ,0,1$ and each term afterwards is given by the linear recurrence 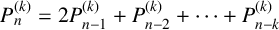 $P^{(k)}_n=2P^{(k)}_{n-1}+P^{(k)}_{n-2}+\cdots +P^{(k)}_{n-k}$. For the Pell sequence, the formula
$P^{(k)}_n=2P^{(k)}_{n-1}+P^{(k)}_{n-2}+\cdots +P^{(k)}_{n-k}$. For the Pell sequence, the formula 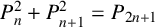 $P^2_n+P^2_{n+1}=P_{2n+1}$ holds for all
$P^2_n+P^2_{n+1}=P_{2n+1}$ holds for all  $n\ge 0$. In this paper, we prove that the Diophantine equation
$n\ge 0$. In this paper, we prove that the Diophantine equation 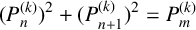 $$ \begin{align*} (P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m \end{align*} $$
$$ \begin{align*} (P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m \end{align*} $$
has no solution in positive integers 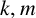 $k, m$ and n with
$k, m$ and n with 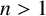 $n>1$ and
$n>1$ and 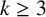 $k\ge 3$.
$k\ge 3$.
This research was supported by ADA University Faculty Research and Development Funds.