Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-05T07:30:10.619Z Has data issue: false hasContentIssue false
  • English
  • Français

ON PSEUDO-NULLITY OF THE FINE MORDELL–WEIL GROUP

Part of: Algebraic number theory: local and $p$-adic fields Algebraic number theory: global fields Arithmetic algebraic geometry

Published online by Cambridge University Press:  03 February 2025

MENG FAI LIM Open the ORCID record for MENG FAI LIM [Opens in a new window] ,
CHAO QIN Open the ORCID record for CHAO QIN [Opens in a new window]  and
JUN WANG
MENG FAI LIM
Affiliation:
School of Mathematics and Statistics, Central China Normal University, Wuhan 430079, PR China e-mail: [email protected]
CHAO QIN*
Affiliation:
College of Mathematical Sciences, Harbin Engineering University, Harbin 150001, PR China
JUN WANG
Affiliation:
Institute for Advanced Study in Mathematics of HIT, Harbin Insitute of Technology, Harbin 150001, PR China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let E be an elliptic curve defined over $\mathbb {Q}$ with good ordinary reduction at a prime 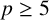$p\geq 5$ and let F be an imaginary quadratic field. Under appropriate assumptions, we show that the Pontryagin dual of the fine Mordell–Weil group of E over the 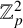$\mathbb {Z}_{p}^2$-extension of F is pseudo-null as a module over the Iwasawa algebra of the group 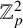$\mathbb {Z}_{p}^2$.

Keywords

fine Mordell–Weil grouppseudo-nullity

MSC classification

Primary: 11G05: Elliptic curves over global fields
Secondary: 11R23: Iwasawa theory 11S25: Galois cohomology
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 9
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Chao Qin’s research is supported by the National Natural Science Foundation of China under Grant No. 12001546, Heilongjiang Province under Grant No. 3236330122 and Harbin Engineering University under Grant No. GK0000020127. Jun Wang’s research is supported by the National Natural Science Foundation of China under Grant No. 12331004.

References

Bertolini, M., ‘Iwasawa theory for elliptic curves over imaginary quadratic fields’, J. Théor. Nombres Bordeaux 13(1) (2001), 1–25.CrossRefGoogle Scholar
Bhave, A., ‘Analogue of Kida’s formula for certain strongly admissible extension’, J. Number Theory 122 (2007), 100–120.CrossRefGoogle Scholar
Coates, J. and Greenberg, R., ‘Kummer theory for abelian varieties over local fields’, Invent. Math. 124(1–3) (1996), 129–174.CrossRefGoogle Scholar
Coates, J. and Sujatha, R., ‘Fine Selmer groups of elliptic curves over $p$ -adic Lie extensions’, Math. Ann. 331(4) (2005), 809–839.CrossRefGoogle Scholar
Hachimori, Y. and Matsuno, K., ‘An analogue of Kida’s formula for the Selmer groups of elliptic curves’, J. Algebraic Geom. 8 (1999), 581–601.Google Scholar
Imai, H., ‘A remark on the rational points of abelian varieties with values in cyclotomic ${\mathbb{Z}}_p$ -extensions’, Proc. Japan Acad. 51 (1975), 12–16.Google Scholar
Jha, S., ‘Fine Selmer group of Hida deformations over non-commutative $p$ -adic Lie extensions’, Asian J. Math. 16(2) (2012), 353–366.CrossRefGoogle Scholar
Lee, J., ‘Structure of the Mordell–Weil group over the ${\mathbb{Z}}_p$ -extensions’, Trans. Amer. Math. Soc. 373(4) (2020), 2399–2425.CrossRefGoogle Scholar
Lei, A., ‘Algebraic structure and characteristic ideals of fine Mordell–Weil groups and plus/minus Mordell–Weil groups’, Math. Z. 303(1) (2023), Article no. 14, 17 pages.CrossRefGoogle Scholar
Lim, M. F., ‘A remark on the ${\mathfrak{M}}_H(G)$ -conjecture and Akashi series’, Int. J. Number Theory 11(1) (2015), 269–297.CrossRefGoogle Scholar
Lim, M. F., ‘On the pseudo-nullity of the dual fine Selmer groups’, Int. J. Number Theory 11(7) (2015), 2055–2063.CrossRefGoogle Scholar
Lim, M. F., ‘Notes on the fine Selmer groups’, Asian J. Math. 21(2) (2017), 337–362.CrossRefGoogle Scholar
Lim, M. F., ‘On the control theorem for fine Selmer groups and the growth of fine Tate–Shafarevich groups in $\mathbb{Z}p$ -extensions’, Doc. Math. 25 (2020), 2445–2471.CrossRefGoogle Scholar
Lim, M. F., ‘Structure of fine Selmer groups over $\mathbb{Z}p$ -extensions’, Math. Proc. Cambridge Philos. Soc. 176(2) (2024), 287–308.CrossRefGoogle Scholar
Lim, M. F., ‘On fine Mordell–Weil groups over $\mathbb{Z}p$ -extensions of an imaginary quadratic field’, Ann. Math. Qué., to appear. Published online (24 December 2024).CrossRefGoogle Scholar
Lim, M. F. and Murty, V. K., ‘The growth of fine Selmer groups’, J. Ramanujan Math. Soc. 31(1) (2016), 79–94.Google Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of Number Fields, 2nd edn, Grundlehren der mathematischen Wissenschaften, 323 (Springer-Verlag, Berlin, 2008).CrossRefGoogle Scholar
Perrin-Riou, B., $p$ -adic $L$ -functions and $p$ -adic Representations, SMF/AMS Texts and Monographs, 3 (American Mathematical Society, Providence, RI; Société Mathématique de France, Paris, 2000), translated from the 1995 French original by Leila Schneps and revised by the author.Google Scholar
Van Order, J., ‘Some remarks on the two-variable main conjecture of Iwasawa theory for elliptic curves without complex multiplication’, J. Algebra 350 (2012), 273–299.CrossRefGoogle Scholar
Venjakob, O., ‘A noncommutative Weierstrass preparation theorem and applications to Iwasawa theory’, J. reine angew. Math. 559 (2003), 153–191.Google Scholar
Wuthrich, C., The Fine Selmer Group and Height Pairings. PhD Thesis (University of Cambridge, 2004).Google Scholar
Wuthrich, C., ‘Iwasawa theory of the fine Selmer group’, J. Algebraic Geom. 16(1) (2007), 83–108.CrossRefGoogle Scholar
Wuthrich, C., ‘The fine Tate–Shafarevich group’, Math. Proc. Cambridge Philos. Soc. 142(1) (2007), 1–12.CrossRefGoogle Scholar