Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-22T05:50:17.191Z Has data issue: false hasContentIssue false
  • English
  • Français

ON PERFECT POWERS AS SUMS OR DIFFERENCES OF TWO k-GENERALISED PELL NUMBERS

Part of: Sequences and sets Diophantine equations Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  20 January 2025

BIJAN KUMAR PATEL Open the ORCID record for BIJAN KUMAR PATEL [Opens in a new window]  and
BIBHU PRASAD TRIPATHY Open the ORCID record for BIBHU PRASAD TRIPATHY [Opens in a new window]
BIJAN KUMAR PATEL
Affiliation:
P. G. Department of Mathematics, Government Women’s College, Sambalpur University, Sundargarh 770001, Odisha, India e-mail: [email protected]
BIBHU PRASAD TRIPATHY*
Affiliation:
Department of Mathematics, School of Applied Sciences, KIIT University, Bhubaneswar 751024, Odisha, India
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For an integer 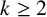$k \geq 2$, let 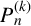$P_{n}^{(k)}$ be the k-generalised Pell sequence, which starts with 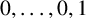$0, \ldots ,0,1$ (k terms), and each term thereafter is given by the recurrence 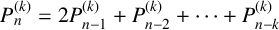$P_{n}^{(k)} = 2 P_{n-1}^{(k)} +P_{n-2}^{(k)} +\cdots +P_{n-k}^{(k)}$. We search for perfect powers, which are sums or differences of two k-generalised Pell numbers.

Keywords

k-generalised Pell numberslinear forms in logarithmsreduction method

MSC classification

Primary: 11B39: Fibonacci and Lucas numbers and polynomials and generalizations
Secondary: 11D61: Exponential equations 11J86: Linear forms in logarithms; Baker's method
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 10
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aboudja, H., Hernane, M., Rihane, S. E. and Togbé, A., ‘On perfect powers that are sums of two Pell numbers’, Period. Math. Hungar. 82 (2021), 11–15.CrossRefGoogle Scholar
Baker, A. and Davenport, H., ‘The equations $3{x}^2-2={y}^2$ and $8{x}^2-7={z}^2$ ’, Q. J. Math. Oxf. Ser. (2) 20 (1969), 129–137.CrossRefGoogle Scholar
Bravo, J. J. and Herrera, J. L., ‘Fibonacci numbers in generalized Pell sequences’, Math. Slovaca 70(5) (2020), 1057–1068.CrossRefGoogle Scholar
Bravo, J. J. and Herrera, J. L., ‘Repdigits in generalized Pell sequences’, Arch. Math. (Brno) 56(4) (2020), 249–262.CrossRefGoogle Scholar
Bravo, J. J., Herrera, J. L. and Luca, F., ‘Common values of generalized Fibonacci and Pell sequences’, J. Number Theory 226 (2021), 51–71.CrossRefGoogle Scholar
Bravo, J. J., Herrera, J. L. and Luca, F., ‘On a generalization of the Pell sequence’, Math. Bohem. 146(2) (2021), 199–213.CrossRefGoogle Scholar
Bugeaud, Y., Mignotte, M. and Siksek, S., ‘Classical and modular approaches to exponential Diophantine equations. I. Fibonacci and Lucas perfect powers’, Ann. of Math. (2) 163(3) (2006), 969–1018.CrossRefGoogle Scholar
Dujella, A. and Pethö, A., ‘A generalization of a theorem of Baker and Davenport’, Quart. J. Math. Oxf. Ser. (2) 49(195) (1998), 291–306.CrossRefGoogle Scholar
Kebli, S., Kihel, O., Larone, J. and Luca, F., ‘On the nonnegative integer solutions to the equation ${F}_n\pm {F}_m={y}^a$ ’, J. Number Theory 220 (2021), 107–127.CrossRefGoogle Scholar
Kihel, O. and Larone, J., ‘On the nonnegative integer solutions of the equation ${F}_n\pm {F}_m={y}^a$ ’, Quaest. Math. 44(8) (2021), 1133–1139.CrossRefGoogle Scholar
Matveev, E. M., ‘An explicit lower bound for a homogeneous rational linear form in the logarithms of algebraic numbers II’, Izv. Mat. 64(6) (2000), 1217–1269.CrossRefGoogle Scholar
Pethö, A., ‘The Pell sequence contains only trivial perfect powers’, Coll. Math. Soc. J. Bolyai 60 (1991), 561–568.Google Scholar
Sanchez, S. G. and Luca, F., ‘Linear combinations of factorials and $S$ -units in a binary recurrence sequence’, Ann. Math. Qué. 38 (2014), 169–188.Google Scholar
Şiar, Z., Keskin, R. and Oztas, E. S., ‘On perfect powers in $k$ -generalized Pell sequence’, Math. Bohem. 148(4), (2023), 507–518.CrossRefGoogle Scholar