Let 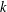$k$ be a finite field and 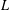$L$ be the function field of a curve 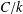$C/k$ of genus 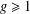$g\geq 1$. In the first part of this note we show that the number of separable 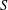$S$-integral points on a constant elliptic curve 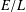$E/L$ is bounded solely in terms of 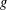$g$ and the size of 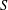$S$. In the second part we assume that 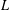$L$ is the function field of a hyperelliptic curve 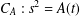$C_{A}:s^{2}=A(t)$, where 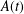$A(t)$ is a square-free 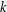$k$-polynomial of odd degree. If $\infty$ is the place of 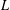$L$ associated to the point at infinity of 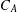$C_{A}$, then we prove that the set of separable 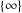$\{\infty \}$-points can be bounded solely in terms of 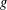$g$ and does not depend on the Mordell–Weil group 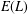$E(L)$. This is done by bounding the number of separable integral points over 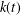$k(t)$ on elliptic curves of the form 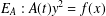$E_{A}:A(t)y^{2}=f(x)$, where 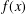$f(x)$ is a polynomial over 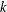$k$. Additionally, we show that, under an extra condition on 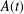$A(t)$, the existence of a separable integral point of ‘small’ height on the elliptic curve 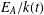$E_{A}/k(t)$ determines the isomorphism class of the elliptic curve 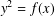$y^{2}=f(x)$.