No CrossRef data available.
Published online by Cambridge University Press: 12 April 2021
Let k and l be positive integers satisfying 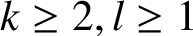 $k \ge 2, l \ge 1$
. A set
$k \ge 2, l \ge 1$
. A set
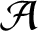 $\mathcal {A}$
of positive integers is an asymptotic basis of order k if every large enough positive integer can be represented as the sum of k terms from
$\mathcal {A}$
of positive integers is an asymptotic basis of order k if every large enough positive integer can be represented as the sum of k terms from
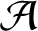 $\mathcal {A}$
. About 35 years ago, P. Erdős asked: does there exist an asymptotic basis of order k where all the subset sums with at most l terms are pairwise distinct with the exception of a finite number of cases as long as
$\mathcal {A}$
. About 35 years ago, P. Erdős asked: does there exist an asymptotic basis of order k where all the subset sums with at most l terms are pairwise distinct with the exception of a finite number of cases as long as
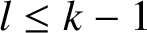 $l \le k - 1$
? We use probabilistic tools to prove the existence of an asymptotic basis of order
$l \le k - 1$
? We use probabilistic tools to prove the existence of an asymptotic basis of order
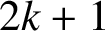 $2k+1$
for which all the sums of at most k elements are pairwise distinct except for ‘small’ numbers.
$2k+1$
for which all the sums of at most k elements are pairwise distinct except for ‘small’ numbers.
The first author was supported by the National Research, Development and Innovation Office NKFIH Grant Nos. K115288 and K129335. This paper was supported by a János Bolyai Research Scholarship of the Hungarian Academy of Sciences, by the ÚNKP-19-4 New National Excellence Program of the Ministry for Innovation and Technology and by the ÚNKP-20-5 New National Excellence Program of the Ministry for Innovation and Technology from the source of the National Research, Development and Innovation Fund.