Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-03T03:36:07.177Z Has data issue: false hasContentIssue false
  • English
  • Français

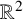ON ARITHMETIC SUMS OF CONNECTED SETS IN $\mathbb {R}^2$

Part of: Special properties Fairly general properties

Published online by Cambridge University Press:  13 January 2023

YU-FENG WU Open the ORCID record for YU-FENG WU [Opens in a new window]
YU-FENG WU*
Affiliation:
School of Mathematics and Statistics, Central South University, Changsha 410085, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that for two connected sets 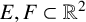$E,F\subset \mathbb {R}^2$ with cardinalities greater than 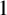$1$ , if one of E and F is compact and not a line segment, then the arithmetic sum $E+F$ has nonempty interior. This improves a recent result of Banakh et al. [‘The continuity of additive and convex functions which are upper bounded on non-flat continua in $\mathbb {R}^n$ ’, Topol. Methods Nonlinear Anal. 54(1)(2019), 247–256] in dimension two by relaxing their assumption that E and F are both compact.

Keywords

arithmetic sumconnected setsinterior

MSC classification

Primary: 54F15: Continua and generalizations
Secondary: 54D05: Connected and locally connected spaces (general aspects) 54D30: Compactness
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 3 , June 2023 , pp. 507 - 519
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlfors, L. V., Complex Analysis. An Introduction to the Theory of Analytic Functions of One Complex Variable, 3rd edn (McGraw-Hill, New York, 1978).Google Scholar
Astels, S., ‘Cantor sets and numbers with restricted partial quotients’, Trans. Amer. Math. Soc. 352(1) (2000), 133–170.CrossRefGoogle Scholar
Banakh, T., Jabłońska, E. and Jabłoński, W., ‘The continuity of additive and convex functions which are upper bounded on non-flat continua in 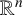${\mathbb{R}}^n$ ’, Topol. Methods Nonlinear Anal. 54(1) (2019), 247–256.Google Scholar
Borwein, J. M. and Lewis, A. S., Convex Analysis and Nonlinear Optimization. Theory and Examples, 2nd edn (Springer, New York, 2006).Google Scholar
Chang, A., ‘On the Minkowski sum of two curves’, Real Anal. Exchange 43(1) (2018), 221–222.CrossRefGoogle Scholar
Feng, D.-J. and Wu, Y.-F., ‘On arithmetic sums of fractal sets in ${\mathbb{R}}^d$ ’, J. Lond. Math. Soc. (2) 104(1) (2021), 35–65.CrossRefGoogle Scholar
Hall, M. J., ‘On the sum and product of continued fractions’, Ann. of Math. (2) 48(2) (1947), 966–993.CrossRefGoogle Scholar
Jones, F. B., ‘Connected and disconnected plane sets and the functional equation $f\left(x+y\right)=f(x)+f(y)$ ’, Bull. Amer. Math. Soc. (N.S.) 48(2) (1942), 115–120.CrossRefGoogle Scholar
Newhouse, S. E., ‘The abundance of wild hyperbolic sets and nonsmooth stable sets for diffeomorphisms’, Publ. Math. Inst. Hautes Études Sci. 50 (1979), 101–151.CrossRefGoogle Scholar
Oxtoby, C. J., Measure and Category: A Survey of the Analogies between Topological and Measure Spaces, 2nd edn (Springer, New York–Berlin, 1980).CrossRefGoogle Scholar
Rockafellar, R. T., Convex Analysis, Princeton Mathematical Series, 28 (Princeton University Press, Princeton, NJ, 1970).CrossRefGoogle Scholar
Rosen, H., ‘An earlier fractal graph’, Real Anal. Exchange 43(2) (2018), 451–454.CrossRefGoogle Scholar
Simon, K. and Taylor, K., ‘Interior of sums of planar sets and curves’, Math. Proc. Cambridge Philos. Soc. 168(1) (2020), 119–148.CrossRefGoogle Scholar
Simon, K. and Taylor, K., ‘Dimension and measure of sums of planar sets and curves’, Mathematika 68 (2022), 1364–1392.CrossRefGoogle Scholar
Steinhaus, H., ‘A new property of G. Cantor’s set’, Wektor 6 (1917), 105–107 (in Polish).Google Scholar
Vietoris, L., ‘Stetige Mengen’, Monatsh. Math. Phys. 31(1) (1921), 173–204.CrossRefGoogle Scholar