Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-08T18:58:41.482Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A CONJECTURE ON THE PERMUTATION CHARACTERS OF FINITE PRIMITIVE GROUPS

Part of: Permutation groups

Published online by Cambridge University Press:  22 October 2019

PABLO SPIGA Open the ORCID record for PABLO SPIGA [Opens in a new window]
PABLO SPIGA*
Affiliation:
Dipartimento di Matematica e Applicazioni,University of Milano-Bicocca, Via Cozzi 55, 20125 Milano, Italy email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 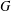$G$ be a finite group with two primitive permutation representations on the sets 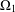$\unicode[STIX]{x1D6FA}_{1}$ and 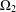$\unicode[STIX]{x1D6FA}_{2}$ and let 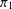$\unicode[STIX]{x1D70B}_{1}$ and 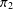$\unicode[STIX]{x1D70B}_{2}$ be the corresponding permutation characters. We consider the case in which the set of fixed-point-free elements of 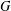$G$ on 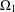$\unicode[STIX]{x1D6FA}_{1}$ coincides with the set of fixed-point-free elements of 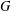$G$ on 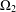$\unicode[STIX]{x1D6FA}_{2}$, that is, for every 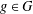$g\in G$, 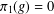$\unicode[STIX]{x1D70B}_{1}(g)=0$ if and only if 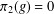$\unicode[STIX]{x1D70B}_{2}(g)=0$. We have conjectured in Spiga [‘Permutation characters and fixed-point-free elements in permutation groups’, J. Algebra299(1) (2006), 1–7] that under this hypothesis either 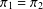$\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70B}_{2}$ or one of $\unicode[STIX]{x1D70B}_{1}-\unicode[STIX]{x1D70B}_{2}$ and 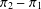$\unicode[STIX]{x1D70B}_{2}-\unicode[STIX]{x1D70B}_{1}$ is a genuine character. In this paper we give evidence towards the veracity of this conjecture when the socle of 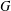$G$ is a sporadic simple group or an alternating group. In particular, the conjecture is reduced to the case of almost simple groups of Lie type.

Keywords

finite primitive groupsfixed-point-free elements

MSC classification

Primary: 20B15: Primitive groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 1 , August 2020 , pp. 77 - 90
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbott, R., Bray, J., Linton, S., Nickerson, S., Norton, S., Parker, R., Suleiman, I., Tripp, J., Walsh, P. and Wilson, R., AtlasRep—a GAP Package, Version 2.1.0, 2019, available online at http://www.math.rwth-aachen.de/∼Thomas.Breuer/atlasrep/doc/manual.pdf.Google Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., Atlas of Finite Groups. Maximal Subgroups and Ordinary Characters for Simple Groups (Oxford University Press, Eynsham, 1985), with computational assistance from J. G. Thackray.Google Scholar
Dixon, J. D. and Mortimer, B., Permutation Groups, Graduate Texts in Mathematics, 163 (Springer, New York, 1996).10.1007/978-1-4612-0731-3CrossRefGoogle Scholar
Förster, P. and Kovács, L. G., ‘A problem of Wielandt on finite permutation groups’, J. Lond. Math. Soc. (2) 41(2) (1990), 231–243.10.1112/jlms/s2-41.2.231CrossRefGoogle Scholar
The GAP Group, GAP—Groups, Algorithms, and Programming, Version 4.8.7, 2017, available online at https://www.gap-system.org/Releases/4.8.7.html.Google Scholar
Giudici, M., Praeger, C. E. and Spiga, P., ‘Finite primitive permutation groups and regular cycles of their elements’, J. Algebra 421 (2015), 27–55.10.1016/j.jalgebra.2014.08.015CrossRefGoogle Scholar
Gorenstein, D., Lyons, R. and Solomon, R., The Classification of the Finite Simple Groups, Number 3, Mathematical Surveys and Monographs, 40 (American Mathematical Society, Providence, RI, 1998), Part I, Ch. A, Almost Simple K-Groups.Google Scholar
Guest, S., Morris, J., Praeger, C. E. and Spiga, P., ‘Affine transformations of finite vector spaces with large orders or few cycles’, J. Pure Appl. Algebra 219(2) (2015), 308–330.10.1016/j.jpaa.2014.04.023CrossRefGoogle Scholar
Guest, S., Morris, J., Praeger, C. E. and Spiga, P., ‘On the maximum orders of elements of finite almost simple groups and primitive permutation groups’, Trans. Amer. Math. Soc. 367(11) (2015), 7665–7694.CrossRefGoogle Scholar
Guest, S., Morris, J., Praeger, C. E. and Spiga, P., ‘Finite primitive permutation groups containing a permutation having at most four cycles’, J. Algebra 454 (2016), 233–251.CrossRefGoogle Scholar
Guest, S. and Spiga, P., ‘Finite primitive groups and regular orbits of group elements’, Trans. Amer. Math. Soc. 369(2) (2017), 997–1024.CrossRefGoogle Scholar
Guralnick, R. M., ‘Subgroups of prime power index in a simple group’, J. Algebra 81(2) (1983), 304–311.10.1016/0021-8693(83)90190-4CrossRefGoogle Scholar
Guralnick, R. M. and Saxl, J., ‘Primitive permutation characters’, in: Groups, Combinatorics and Geometry (Durham, 1990), London Mathematical Society Lecture Note Series, 165 (Cambridge University Press, Cambridge, 1992), 364–367.10.1017/CBO9780511629259.032CrossRefGoogle Scholar
Holmes, E. and Wilson, R. A., personal communication.Google Scholar
Kimmerle, W., Lyons, R., Sandling, R. and Teague, D. N., ‘Composition factors from the group ring and Artin’s theorem on orders of simple groups’, Proc. Lond. Math. Soc. (3) 60(1) (1990), 89–122.10.1112/plms/s3-60.1.89CrossRefGoogle Scholar
Klingen, N., Arithmetical Similarities. Prime Decomposition and Finite Group Theory, Oxford Mathematical Monographs (The Clarendon Press–Oxford University Press, New York, 1998).Google Scholar
Li, C. H. and Li, X., ‘On permutation groups of degree a product of two prime-powers’, Comm. Algebra 42(11) (2014), 4722–4743.CrossRefGoogle Scholar
Liebeck, M. W., Praeger, C. E. and Saxl, J., ‘A classification of the maximal subgroups of the finite alternating and symmetric groups’, J. Algebra 111(2) (1987), 365–383.CrossRefGoogle Scholar
Mazurov, V. D., Merzlyakov, Y. I. and Churkin, V. D. (eds.), The Kourovka Notebook, Unsolved Problems in Group Theory, American Mathematical Society Translations, Ser. 2, 121 (American Mathematical Society, Providence, RI, 1983), translated from the Russian by D. J. Johnson.Google Scholar
Perlis, R., ‘On the equation 𝜁K(s) =𝜁 K ′(s)’, J. Number Theory 9(3) (1977), 342–360.10.1016/0022-314X(77)90070-1CrossRefGoogle Scholar
Spiga, P., ‘Permutation characters and fixed-point-free elements in permutation groups’, J. Algebra 299(1) (2006), 1–7.10.1016/j.jalgebra.2006.03.015CrossRefGoogle Scholar
Wilson, R. A., ‘Maximal subgroups of sporadic groups’, in: Finite Simple Groups: Thirty Years of the Atlas and Beyond, Contemporary Mathematics, 694 (American Mathematical Society, Providence, RI, 2017), 57–72.10.1090/conm/694/13974CrossRefGoogle Scholar