Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-05-07T05:43:59.770Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A CONJECTURE FOR A REFINEMENT OF THE SUM OF MINIMAL EXCLUDANTS

Part of: Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  20 July 2023

JULIA Q. D. DU  and
DAZHAO TANG Open the ORCID record for DAZHAO TANG [Opens in a new window]
JULIA Q. D. DU
Affiliation:
School of Mathematical Sciences, Hebei Workstation for Foreign Academicians, Hebei Normal University, Shijiazhuang 050024, PR China e-mail: [email protected]
DAZHAO TANG*
Affiliation:
School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In 2019, Andrews and Newman [‘Partitions and the minimal excludant’, Ann. Comb. 23(2) (2019), 249–254] introduced the arithmetic function 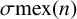$\sigma \textrm {mex}(n)$, which denotes the sum of minimal excludants over all the partitions of n. Baruah et al. [‘A refinement of a result of Andrews and Newman on the sum of minimal excludants’, Ramanujan J., to appear] showed that the sum of minimal excludants over all the partitions of n is the same as the number of partition pairs of n into distinct parts. They proved three congruences modulo 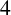$4$ and 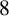$8$ for two functions appearing in this refinement and conjectured two further congruences modulo 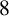$8$ and 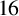$16$. We confirm these two conjectures by using q-series manipulations and modular forms.

Keywords

congruencespartitionsminimal excludantmodular formsrefinement

MSC classification

Primary: 11P83: Partitions; congruences and congruential restrictions
Secondary: 05A17: Partitions of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 2 , April 2024 , pp. 276 - 287
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Julia Q. D. Du was partially supported by the National Natural Science Foundation of China (No. 12201177), the Hebei Natural Science Foundation (No. A2021205018), the Science and Technology Project of Hebei Education Department (No. BJK2023092), the Doctor Foundation of Hebei Normal University (No. L2021B02), the Program for Foreign Experts of Hebei Province and the Program for 100 Foreign Experts Plan of Hebei Province. Dazhao Tang was partially supported by the National Natural Science Foundation of China (No. 12201093), the Natural Science Foundation Project of Chongqing CSTB (No. CSTB2022NSCQ-MSX0387), the Science and Technology Research Program of Chongqing Municipal Education Commission (No. KJQN202200509) and the Doctoral start-up research Foundation (No. 21XLB038) of Chongqing Normal University.

References

Andrews, G. E. and Berndt, B. C., Ramanujan’s Lost Notebook, Part I (Springer, New York, 2005).CrossRefGoogle Scholar
Andrews, G. E., Berndt, B. C., Chan, S. H., Kim, S. and Malik, A., ‘Four identities and third order mock theta functions’, Nagoya Math. J. 239 (2020), 173–204.CrossRefGoogle Scholar
Andrews, G. E. and Newman, D., ‘Partitions and the minimal excludant’, Ann. Comb. 23(2) (2019), 249–254.CrossRefGoogle Scholar
Ballantine, C. and Merca, M., ‘Combinatorial proof of the minimal excludant theorem’, Int. J. Number Theory 17(8) (2021), 1765–1779.CrossRefGoogle Scholar
Baruah, N. D., Bhoria, S. C., Eyyunni, P. and Maji, B., ‘A refinement of a result of Andrews and Newman on the sum of minimal excludants’, Ramanujan J., to appear. Published online (14 June 2023).CrossRefGoogle Scholar
Berndt, B. C., Ramanujan’s Notebooks, Part III (Springer-Verlag, New York, 1991).CrossRefGoogle Scholar
Cotron, T., Michaelsen, A., Stamm, E. and Zhu, W., ‘Lacunary eta-quotients modulo powers of primes’, Ramanujan J. 53(2) (2020), 269–284.CrossRefGoogle Scholar
Diamond, F. and Shurman, J., A First Course in Modular Forms, Graduate Texts in Mathematics, 228 (Springer-Verlag, New York, 2005).Google Scholar
Fraenkel, A. S. and Peled, U., ‘Harnessing the unwieldy MEX function’, in: Games of No Chance 4, Mathematical Sciences Research Institute Publications, 63 (ed. Nowakowski, R. J.) (Cambridge University Press, New York, 2015), 77–94.Google Scholar
Frye, J. and Garvan, F., ‘Automatic proof of theta-function identities’, in: Elliptic Integrals, Elliptic Functions and Modular Forms in Quantum Field Theory, Texts & Monographs in Symbolic Computation (eds. Blümlein, J., Schneider, C. and Paule, P.) (Springer, Cham, 2019), 195–258.CrossRefGoogle Scholar
Grabner, P. J. and Knopfmacher, A., ‘Analysis of some new partition statistics’, Ramanujan J. 12(3) (2006), 439–454.CrossRefGoogle Scholar
Robins, S., ‘Generalized Dedekind $\eta$ -products’, in: The Rademacher Legacy to Mathematics (University Park, PA, 1992), Contemporary Mathematics, 166 (eds. Andrews, G. E., Bressoud, D. M. and Parson, L. A.) (American Mathematical Society, Providence, RI, 1994), 119–128.CrossRefGoogle Scholar
Schoeneberg, B., Elliptic Modular Functions: An Introduction, Die Grundlehren der Mathematischen Wissenschaften, 203 (Springer-Verlag, New York–Heidelberg, 1974).CrossRefGoogle Scholar
Sturm, J., ‘On the congruence of modular forms’, in: Number Theory, Lecture Notes in Mathematics, 1240 (eds. Chudnovsky, D. V., Chudnovsky, G. V., Cohn, H. and Nathanson, M. B.) (Springer, Berlin, 1987), 275–280.CrossRefGoogle Scholar
Tang, D., ‘Proof of a conjecture of Banerjee and Dastidar on odd crank’, Bull. Aust. Math. Soc., to appear. Published online (13 January 2023); doi:10.1017/S0004972722001678.CrossRefGoogle Scholar
Yao, O. X. M., Xia, E. X. W., ‘New Ramanujan-like congruences modulo powers of 2 and 3 for overpartitions’, J. Number Theory 133(6) (2013), 1932–1949.CrossRefGoogle Scholar