Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-22T13:36:06.794Z Has data issue: false hasContentIssue false
  • English
  • Français

THE NUMBER OF PAIRWISE NONCOMMUTING SETS IN A FINITE GROUP

Part of: Representation theory of groups

Published online by Cambridge University Press:  17 February 2025

YONG YANG Open the ORCID record for YONG YANG [Opens in a new window]  and
MOHAMMAD ZARRIN Open the ORCID record for MOHAMMAD ZARRIN [Opens in a new window]
YONG YANG
Affiliation:
Department of Mathematics, Texas State University, 601 University Drive, San Marcos, TX 78666, USA e-mail: [email protected]
MOHAMMAD ZARRIN*
Affiliation:
Department of Mathematics, Texas State University, 601 University Drive, San Marcos, TX 78666, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We say that two nonempty subsets A and B with cardinality r of a group G are noncommuting subsets if 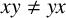$xy\neq yx$ for every $x\in A$ and 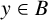$y\in B$. We say a nonempty set 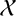$\mathcal {X}$ of subsets with cardinality r of G is an r-noncommuting set if every two elements of 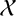$\mathcal {X}$ are noncommuting subsets. If 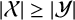$|\mathcal {X}| \geq |\mathcal {Y}|$ for any other r-noncommuting set 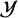$\mathcal {Y}$ of G, then the cardinality of 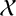$\mathcal {X}$ (if it exists) is denoted by 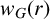$w_G(r)$ and is called the r-clique number of G. In this paper, we try to find the influence of the function 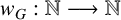$w_G: \mathbb {N} \longrightarrow \mathbb {N}$ on the structure of groups.

Keywords

pairwise noncommuting setssolvable groups

MSC classification

Primary: 20D60: Arithmetic and combinatorial problems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 8
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This project was supported by a grant to the first author from the Simons Foundation (No. 918096).

References

Bertram, E. A., ‘Some applications of graph theory to finite groups’, Discrete Math. 44 (1983), 31–43.CrossRefGoogle Scholar
Chin, A. Y. M., ‘On non-commuting sets in an extraspecial $p$ -group’, J. Group Theory 8 (2005), 189–194.CrossRefGoogle Scholar
Guralnick, R. and Robinson, G., ‘On the commuting probability in finite groups’, J. Algebra 300 (2006), 509–528.CrossRefGoogle Scholar
Pyber, L., ‘The number of pairwise non-commuting elements and the index of the centre in a finite group’, J. Lond. Math. Soc. (2) 35(2) (1987), 287–295.CrossRefGoogle Scholar
Zarrin, M., ‘On noncommuting sets and centralisers in infinite groups’, Bull. Aust. Math. Soc. 93 (2016), 42–46.CrossRefGoogle Scholar