Article contents
NOWHERE-ZERO 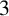 $3$-FLOWS IN TWO FAMILIES OF VERTEX-TRANSITIVE GRAPHS
$3$-FLOWS IN TWO FAMILIES OF VERTEX-TRANSITIVE GRAPHS
Published online by Cambridge University Press: 15 September 2022
Abstract
Let
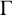 $\Gamma $
be a graph of valency at least four whose automorphism group contains a minimally vertex-transitive subgroup G. It is proved that
$\Gamma $
be a graph of valency at least four whose automorphism group contains a minimally vertex-transitive subgroup G. It is proved that
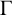 $\Gamma $
admits a nowhere-zero
$\Gamma $
admits a nowhere-zero
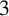 $3$
-flow if one of the following two conditions holds: (i)
$3$
-flow if one of the following two conditions holds: (i)
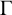 $\Gamma $
is of order twice an odd number and G contains a central involution; (ii) G is a direct product of a
$\Gamma $
is of order twice an odd number and G contains a central involution; (ii) G is a direct product of a
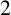 $2$
-subgroup and a subgroup of odd order.
$2$
-subgroup and a subgroup of odd order.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by the Basic Research and Frontier Exploration Project of Chongqing (No. cstc2018jcyjAX0010) and the Foundation of Chongqing Normal University (21XLB006).
References
- 3
- Cited by



