Hostname: page-component-6dbcb7884d-t8hx9 Total loading time: 0 Render date: 2025-02-14T08:45:05.096Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE NUMBER OF SOLUTIONS OF TERNARY PURELY EXPONENTIAL DIOPHANTINE EQUATIONS

Part of: Diophantine equations

Published online by Cambridge University Press:  10 June 2022

YASUTSUGU FUJITA Open the ORCID record for YASUTSUGU FUJITA [Opens in a new window] ,
MAOHUA LE Open the ORCID record for MAOHUA LE [Opens in a new window]  and
NOBUHIRO TERAI Open the ORCID record for NOBUHIRO TERAI [Opens in a new window]
YASUTSUGU FUJITA*
Affiliation:
Department of Mathematics, College of Industrial Technology, Nihon University, 2-11-1 Shin-ei, Narashino, Chiba, Japan
MAOHUA LE
Affiliation:
Institute of Mathematics, Lingnan Normal College, Zhangjiang, Guangdong 524048, PR China e-mail: [email protected]
NOBUHIRO TERAI
Affiliation:
Division of Mathematical Sciences, Department of Integrated Science and Technology, Faculty of Science and Technology, Oita University, 700, Dannoharu, Oita 870–1192, Japan e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

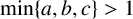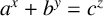Let a, b, c be fixed coprime positive integers with $\min \{a,b,c\}>1$ . We discuss the conjecture that the equation $a^{x}+b^{y}=c^{z}$ has at most one positive integer solution 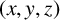$(x,y,z)$ with 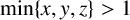$\min \{x,y,z\}>1$ , which is far from solved. For any odd positive integer r with 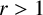$r>1$ , let 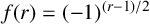$f(r)=(-1)^{(r-1)/2}$ and 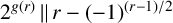$2^{g(r)}\,\|\, r-(-1)^{(r-1)/2}$ . We prove that if one of the following conditions is satisfied, then the conjecture is true: (i) 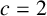$c=2$ ; (ii) a, b and c are distinct primes; (iii) 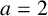$a=2$ and either 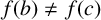$f(b)\ne f(c)$ , or 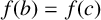$f(b)=f(c)$ and 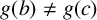$g(b)\ne g(c)$ .

Keywords

ternary purely exponential Diophantine equationupper bound for number of solutionsTerai–Jeśmanowicz conjecture

MSC classification

Primary: 11D61: Exponential equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 1 , February 2023 , pp. 53 - 65
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The third author is supported by JSPS KAKENHI Grant Number 18K03247.

References

Bennett, M. A. and Skinner, C. M., ‘Ternary Diophantine equations via Galois representations and modular forms’, Canad. J. Math. 56 (2004), 23–54.CrossRefGoogle Scholar
Beukers, F. and Schlickewei, H. P., ‘The equation $x+y = 1$ in finitely generated groups’, Acta Arith. 78 (1996), 189–199.10.4064/aa-78-2-189-199CrossRefGoogle Scholar
Bilu, Y. F., Hanrot, G. and Voutier, P. M., ‘Existence of primitive divisors of Lucas and Lehmer numbers’, J. reine angew. Math. 539 (2001), 75–122 (with an appendix by M. Mignotte).Google Scholar
Bugeaud, Y., ‘Linear forms in $p$ -adic logarithms and the Diophantine equation $\left({x}^n-1\right)/\left(x-1\right) = {y}^q$ ’, Math. Proc. Cambridge Philos. Soc. 127 (1999), 373–381.10.1017/S0305004199003692CrossRefGoogle Scholar
Cao, Z.-F., ‘On the Diophantine equation ${a}^x+{b}^y = {c}^z$  I’, Chinese Sci. Bull. 31 (1986), 1688–1690 (in Chinese).Google Scholar
Cohn, J. H. E., ‘The Diophantine equation ${x}^2+{2}^k = {y}^n$ ’, Arch. Math. (Basel) 59 (1992), 341–344.CrossRefGoogle Scholar
Gel’fond, A. O., ‘Sur la divisibilité de la différence des puissances de deux nombres entiers par une puissance d’un idéal premier’, Mat. Sb. 7 (1940), 7–25.Google Scholar
Guy, R. K., Unsolved Problems in Number Theory, 3rd edn (Science Press, Beijing, 2007).Google Scholar
Hu, Y.-Z. and Le, M.-H., ‘A note on ternary purely exponential Diophantine equations’, Acta Arith. 171 (2015), 173–182.CrossRefGoogle Scholar
Hu, Y.-Z. and Le, M.-H., ‘An upper bound for the number of solutions of ternary purely exponential Diophantine equations’, J. Number Theory 183 (2018), 62–73.CrossRefGoogle Scholar
Hu, Y.-Z. and Le, M.-H., ‘An upper bound for the number of solutions of ternary purely exponential Diophantine equations II’, Publ. Math. Debrecen 95 (2019), 335–354.CrossRefGoogle Scholar
Jeśmanowicz, L., ‘Several remarks on Pythagorean numbers’, Wiadom. Math. 1 (1955/1956), 196–202 (in Polish).Google Scholar
Laurent, M., ‘Linear forms in two logarithms and interpolation determinants II’, Acta Arith. 133 (2008), 325–348.CrossRefGoogle Scholar
Le, M.-H., ‘On the Diophantine equation ${a}^x+{b}^y = {c}^z$ ’, J. Changchun Teachers College 2 (1985), 50–62 (in Chinese).Google Scholar
Le, M.-H., ‘Some exponential Diophantine equations I: The equation ${D}_1{x}^2-{D}_2{y}^2 = \lambda {k}^z$ ’, J. Number Theory 55 (1995), 209–221.CrossRefGoogle Scholar
Le, M.-H., ‘On Cohn’s conjecture concerning the Diophantine equation ${x}^2+{2}^m = {y}^n$ ’, Arch. Math. (Basel) 78 (2002), 26–35.CrossRefGoogle Scholar
Le, M.-H., Scott, R. and Styer, R., ‘A survey on the ternary purely exponential Diophantine equation ${a}^x+{b}^y = {c}^z$ ’, Surv. Math. Appl. 14 (2019), 109–140.Google Scholar
Mahler, K., ‘Zur Approximation algebraischer Zahlen I: Über den grössten Primtreiler binärer Formen’, Math. Ann. 107 (1933), 691–730.CrossRefGoogle Scholar
Miyazaki, T. and Pink, I., ‘Number of solutions to a special type of unit equations in two variables’, Preprint, 2020, arXiv:2006.15952.Google Scholar
Scott, R., ‘On the equation ${p}^x-{q}^y = c$ and ${a}^x+{b}^y = {c}^z$ ’, J. Number Theory 44 (1993), 153–165.CrossRefGoogle Scholar
Scott, R. and Styer, R., ‘Number of solutions to ${a}^x+{b}^y = {c}^z$ ’, Publ. Math. Debrecen 88 (2016), 131–138.CrossRefGoogle Scholar
Terai, N., ‘The Diophantine equation ${a}^x+{b}^y = {c}^z$ ’, Proc. Japan Acad. Ser. A Math. Sci. 70A (1994), 22–26.Google Scholar
The PARI Group, PARI/GP, version 2.13.3, Bordeaux, 2021, available at http://pari.math.u-bordeaux.fr/.Google Scholar
Voutier, P. M., ‘Primitive divisors of Lucas and Lehmer sequences’, Math. Comp. 64 (1995), 869–888.CrossRefGoogle Scholar