No CrossRef data available.
Published online by Cambridge University Press: 23 June 2023
Let p be a prime and let r, s be positive integers. In this paper, we prove that the Goormaghtigh equation 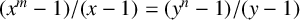 $(x^m-1)/(x-1)=(y^n-1)/(y-1)$,
$(x^m-1)/(x-1)=(y^n-1)/(y-1)$, 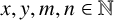 $x,y,m,n \in {\mathbb {N}}$,
$x,y,m,n \in {\mathbb {N}}$, 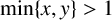 $\min \{x,y\}>1$,
$\min \{x,y\}>1$, 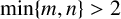 $\min \{m,n\}>2$ with
$\min \{m,n\}>2$ with 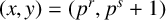 $(x,y)=(p^r,p^s+1)$ has only one solution
$(x,y)=(p^r,p^s+1)$ has only one solution 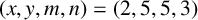 $(x,y,m,n)=(2,5,5,3)$. This result is related to the existence of some partial difference sets in combinatorics.
$(x,y,m,n)=(2,5,5,3)$. This result is related to the existence of some partial difference sets in combinatorics.