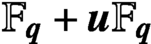Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T01:38:54.954Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON k-GALOIS LCD CODES OVER THE RING $\mathbb {F}_{\mathbf{\mathit{q}}}\boldsymbol{+}\mathbf{\mathit{u}}\mathbb {F}_{\mathbf{\mathit{q}}}$

Part of: Theory of error-correcting codes and error-detecting codes

Published online by Cambridge University Press:  14 December 2020

RONGSHENG WU Open the ORCID record for RONGSHENG WU [Opens in a new window]  and
MINJIA SHI Open the ORCID record for MINJIA SHI [Opens in a new window]
RONGSHENG WU
Affiliation:
Ministry of Education Key Laboratory of Intelligent Computing and Signal Processing, School of Mathematical Sciences, Anhui University, Hefei, Anhui230601, P. R. China e-mail: [email protected]
MINJIA SHI*
Affiliation:
Ministry of Education Key Laboratory of Intelligent Computing and Signal Processing, School of Mathematical Sciences, Anhui University, Hefei, Anhui230601, P. R. China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

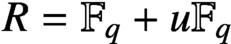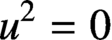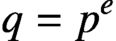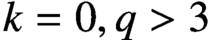We study the k-Galois linear complementary dual (LCD) codes over the finite chain ring $R=\mathbb {F}_q+u\mathbb {F}_q$ with $u^2=0$ , where $q=p^e$ and p is a prime number. We give a sufficient condition on the generator matrix for the existence of k-Galois LCD codes over R. Finally, we show that a linear code over R (for $k=0, q> 3$ ) is equivalent to a Euclidean LCD code, and a linear code over R (for 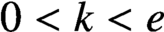$0<k<e$ , 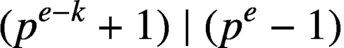$(p^{e-k}+1)\mid (p^e-1)$ and 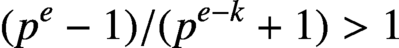${(p^e-1)}/{(p^{e-k}+1)}>1$ ) is equivalent to a k-Galois LCD code.

Keywords

Euclidean LCD codesGray mapk-Galois LCD codeslinear codeslinear complementary dual codes

MSC classification

Primary: 94B05: Linear codes, general
Secondary: 94B15: Cyclic codes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 1 , August 2021 , pp. 154 - 161
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research is supported by the National Natural Science Foundation of China (12071001, 61672036), the Excellent Youth Foundation of Natural Science Foundation of Anhui Province (1808085J20), the Academic Fund for Outstanding Talents in Universities (gxbjZD03) and the Natural Science Foundation of Anhui Provence (2008085QA04).

References

Carlet, C., Mesnager, S., Tang, C., Qi, Y. and Pellikaan, R., ‘Linear codes over ${F}_q$ are equivalent to LCD codes for $q>3$ ’, IEEE Trans. Inform. Theory 64(4) (2018), 3010–3017.CrossRefGoogle Scholar
Chen, B. and Liu, H., ‘New construction of MDS codes with complementary duals’, IEEE Trans. Inform. Theory 64(8) (2018), 5776–5782.CrossRefGoogle Scholar
Dougherty, S., Kim, J., Özkaya, B., Sok, L. and Solé, P., ‘The combinatorics of LCD codes: linear programming bound and orthogonal matrices ’ Int. J. Inf. Coding Theory 4(2–3) (2017), 116–128.Google Scholar
Fan, Y. and Zhang, L., ‘Galois self-dual constacyclic codes’, Des. Codes Cryptogr. 84(3) (2017), 473–492.CrossRefGoogle Scholar
Güneri, C., Özkaya, B. and Solé, P., ‘Quasi-cyclic complementary dual codes’, Finite Fields Appl. 42 (2016), 67–80.CrossRefGoogle Scholar
Jin, L., ‘Construction of MDS codes with complementary duals’, IEEE Trans. Inform. Theory 63(5) (2017), 2843–2847.Google Scholar
Liu, H. and Pan, X., ‘Galois hulls of linear codes over finite fields’, Des. Codes Cryptogr. 88 (2020), 241–255.CrossRefGoogle Scholar
Liu, X., Fan, Y. and Liu, H., ‘Galois LCD codes over finite fields’, Finite Fields Appl. 49 (2018), 227–242.CrossRefGoogle Scholar
Liu, X. and Liu, H., ‘LCD codes over finite chain rings’, Finite Fields Appl. 34 (2015), 1–19.CrossRefGoogle Scholar
Massey, J., ‘Linear codes with complementary dual’, Discrete Math. 106/107 (1992), 337–342.CrossRefGoogle Scholar
Mesnager, S., Tang, C. and Qi, Y., ‘Complementary dual algebraic geometry codes’, IEEE Trans. Inform. Theory 64(4) (2018), 2390–2397.CrossRefGoogle Scholar
Pang, B., Zhu, S. and Sun, Z., ‘On LCD negacyclic codes over finite fields’, J. Syst. Sci. Complex. 31(4) (2018), 1065–1077.CrossRefGoogle Scholar
Sendrier, N., ‘Linear codes with complementary duals meet the Gilbert–Varshamov bound’, Discrete Math. 285(1–3) (2004), 345–347.CrossRefGoogle Scholar
Shi, X., Yue, Q. and Yang, S., ‘New LCD MDS codes constructed from generalized Reed–Solomon codes’, J. Algebra Appl. 18(8) (2019), 1950150.CrossRefGoogle Scholar
Yang, X. and Massey, J., ‘The condition for a cyclic code to have a complementary dual’, Discrete Math. 126 (1994), 391–393.CrossRefGoogle Scholar
Zhu, H. and Shi, M., ‘On linear complementary dual four circulant codes’, Bull. Aust. Math. Soc. 98 (2018), 159–166.CrossRefGoogle Scholar