No CrossRef data available.
Article contents
A NOTE ON GROUP RINGS WITH TRIVIAL UNITS
Published online by Cambridge University Press: 19 July 2021
Abstract
Let R be a ring with identity of characteristic two and G a nontrivial torsion group. We show that if the units in the group ring 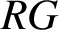 $RG$
are all trivial, then G must be cyclic of order two or three. We also consider the case where R is a commutative ring with identity of odd prime characteristic and G is a nontrivial locally finite group. We show that in this case, if the units in
$RG$
are all trivial, then G must be cyclic of order two or three. We also consider the case where R is a commutative ring with identity of odd prime characteristic and G is a nontrivial locally finite group. We show that in this case, if the units in 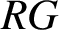 $RG$
are all trivial, then G must be cyclic of order two. These results improve on a result of Herman et al. [‘Trivial units for group rings with G-adapted coefficient rings’, Canad. Math. Bull.48(1) (2005), 80–89].
$RG$
are all trivial, then G must be cyclic of order two. These results improve on a result of Herman et al. [‘Trivial units for group rings with G-adapted coefficient rings’, Canad. Math. Bull.48(1) (2005), 80–89].
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.



