Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T15:07:35.830Z Has data issue: false hasContentIssue false
  • English
  • Français

NOTE ON FOURIER–STIELTJES COEFFICIENTS OF COIN-TOSSING MEASURES

Part of: Foundations of probability theory Diophantine approximation, transcendental number theory Harmonic analysis in one variable

Published online by Cambridge University Press:  20 April 2020

XIANG GAO Open the ORCID record for XIANG GAO [Opens in a new window]  and
SHENGYOU WEN Open the ORCID record for SHENGYOU WEN [Opens in a new window]
XIANG GAO*
Affiliation:
Department of Mathematics, Hubei Key Laboratory of Applied Mathematics, Hubei University, Wuhan, 430062, PR China email [email protected]
SHENGYOU WEN
Affiliation:
Department of Mathematics, Hubei Key Laboratory of Applied Mathematics, Hubei University, Wuhan, 430062, PR China email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is known that the Fourier–Stieltjes coefficients of a nonatomic coin-tossing measure may not vanish at infinity. However, we show that they could vanish at infinity along some integer subsequences, including the sequence 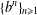${\{b^{n}\}}_{n\geq 1}$ where 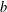$b$ is multiplicatively independent of 2 and the sequence given by the multiplicative semigroup generated by 3 and 5. The proof is based on elementary combinatorics and lower-bound estimates for linear forms in logarithms from transcendental number theory.

Keywords

Fourier–Stieltjes coefficientscoin-tossing measureslinear forms in logarithms

MSC classification

Primary: 42A38: Fourier and Fourier-Stieltjes transforms and other transforms of Fourier type
Secondary: 11J86: Linear forms in logarithms; Baker's method 60A10: Probabilistic measure theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 3 , December 2020 , pp. 479 - 489
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author was supported by NSFC (Grant Nos. 11871200 and 11671189).

References

Bisbas, A., ‘A multifractal analysis of an interesting class of measures’, Colloq. Math. 69 (1995), 37–42.10.4064/cm-69-1-37-42CrossRefGoogle Scholar
Bisbas, A., ‘Coin-tossing measures and their Fourier transforms’, J. Math. Anal. Appl. 299 (2004), 550–562.CrossRefGoogle Scholar
Blum, S. R. and Epstein, B., ‘On Fourier transform of an interesting class of measures’, Israel J. Math. 10 (1971), 302–305.CrossRefGoogle Scholar
Blum, S. R. and Epstein, B., ‘On the Fourier–Stieltjes coefficients of Cantor-type distributions’, Israel J. Math. 17 (1974), 35–45.CrossRefGoogle Scholar
Bourgain, J., Lindenstrauss, E., Michel, P. and Venkatesh, A., ‘Some effective results for ×a×b’, Ergodic Theory Dynam. Systems 29(6) (2009), 1705–1722.CrossRefGoogle Scholar
Brown, G., ‘Symmetric Cantor measure, coin-tossing and sum sets’, Tohoku Math. J. (2) 62(4) (2010), 475–483.CrossRefGoogle Scholar
Brown, G. and Moran, W., ‘Coin tossing and powers of singular measures’, Math. Proc. Cambridge Philos. Soc. 77 (1975), 349–364.CrossRefGoogle Scholar
Bugeaud, Y. and Kaneko, H., ‘On the digital representation of smooth numbers’, Math. Proc. Cambridge Philos. Soc. 165(3) (2018), 533–540.CrossRefGoogle Scholar
Cuny, C., Eisner, T. and Farkas, B., ‘Wiener’s lemma along primes and other subsequences’, Adv. Math. 347 (2019), 340–383.CrossRefGoogle Scholar
Fan, A. H. and Lau, K. S., ‘Asymptotic behavior of multiperiodic functions G (x) = ∏ n=1∞g (x/2n)’, J. Fourier Anal. Appl. 4 (1998), 129–150.CrossRefGoogle Scholar
Gao, X., Ma, J. H., Song, K. K. and Zhang, Y. F., ‘Fourier decay rate of coin-tossing type measures’, J. Math. Anal. Appl. 484(1) (2020), Article ID 123706, 14 pages.CrossRefGoogle Scholar
Graham, C. C. and McGehee, O., Essays in Commutative Harmonic Analysis, Grundlehren der mathematischen Wissenschaften, 238 (Springer, New York, 1979).CrossRefGoogle Scholar
Lyons, R., ‘The measure of non-normal sets’, Invent. Math. 83(3) (1986), 605–616.CrossRefGoogle Scholar
Lyons, R., ‘On measures simultaneously 2- and 3-invariant’, Israel J. Math. 61 (1988), 219–224.CrossRefGoogle Scholar
Marsaglia, G., ‘Random variables with independent binary digits’, Ann. Statist. 42 (1971), 1922–1929.CrossRefGoogle Scholar
Matveev, E. M., ‘An explicit lower bound for a homogeneous rational linear form in logarithms of algebraic numbers, II’, Izv. Ross. Acad. Nauk Ser. Mat. 64 (2000), 125–180; (in Russian); English translation in Izv. Math. 64 (2000), 1217–1269.Google Scholar
Pigno, L., ‘Fourier–Stieltjes transforms which vanish at infinity off certain sets’, Glasg. Math. J. 19 (1978), 49–56.CrossRefGoogle Scholar
Salem, R., ‘On singular monotonic functions which are strictly increasing’, Trans. Amer. Math. Soc. 53 (1943), 427–439.CrossRefGoogle Scholar
Stewart, C. L., ‘Sets generated by finite sets of algebraic numbers’, Acta Arith. 184(2) (2018), 193–200.CrossRefGoogle Scholar
Yu, K., ‘p-adic logarithmic forms and group varieties III’, Forum Math. 19 (2007), 187–280.CrossRefGoogle Scholar