No CrossRef data available.
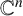 $\mathbb {C}^n$
$\mathbb {C}^n$Published online by Cambridge University Press: 20 January 2022
Every transitive family of subspaces of a vector space of finite dimension
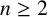 $n\ge 2$
over a field
$n\ge 2$
over a field
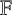 $\mathbb {F}$
contains a subfamily which is transitive but has no proper transitive subfamily. Such a subfamily is called minimally transitive. Each has at most
$\mathbb {F}$
contains a subfamily which is transitive but has no proper transitive subfamily. Such a subfamily is called minimally transitive. Each has at most
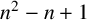 $n^2-n+1$
elements. On
$n^2-n+1$
elements. On
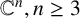 ${{\mathbb {C}}}^n, n\ge 3$
, a minimally transitive family of subspaces has at least four elements and a minimally transitive family of one-dimensional subspaces has
${{\mathbb {C}}}^n, n\ge 3$
, a minimally transitive family of subspaces has at least four elements and a minimally transitive family of one-dimensional subspaces has
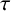 $\tau $
elements where
$\tau $
elements where
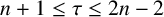 $n+1\le \tau \le 2n-2$
. We show how a minimally transitive family of one-dimensional subspaces arises when it consists of the subspaces spanned by the standard basis vectors together with those spanned by
$n+1\le \tau \le 2n-2$
. We show how a minimally transitive family of one-dimensional subspaces arises when it consists of the subspaces spanned by the standard basis vectors together with those spanned by
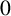 $0$
–
$0$
–
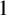 $1$
vectors. On a space of dimension four, the set of nontrivial elements of a medial subspace lattice has five elements if it is minimally transitive. On spaces of dimension
$1$
vectors. On a space of dimension four, the set of nontrivial elements of a medial subspace lattice has five elements if it is minimally transitive. On spaces of dimension
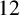 $12$
or more, the set of nontrivial elements of a medial subspace lattice can have six or more elements and be minimally transitive.
$12$
or more, the set of nontrivial elements of a medial subspace lattice can have six or more elements and be minimally transitive.