Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-26T01:44:40.527Z Has data issue: false hasContentIssue false
  • English
  • Français

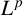$L^p$-BOUNDEDNESS OF THE BEREZIN TRANSFORM ON GENERALISED HARTOGS TRIANGLES

Part of: Special classes of linear operators Holomorphic functions of several complex variables Integral, integro-differential, and pseudodifferential operators

Published online by Cambridge University Press:  04 October 2024

QINGYANG ZOU
QINGYANG ZOU*
Affiliation:
College of Science, Wuhan University of Science and Technology, Wuhan 430081, Hubei, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the 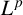$L^p$-boundedness of the Berezin transform on the generalised Hartogs triangles which are defined by

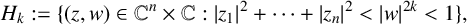$$ \begin{align*}H_k:=\{(z, w)\in\mathbb C^n\times\mathbb C: |z_1|^2+\cdots+|z_n|^2<|w|^{2k}<1\},\end{align*} $$

where 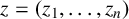$z=(z_1, \ldots , z_n)$ and 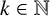$k\in \mathbb N$. We prove that the Berezin transform is bounded on 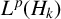$L^p(H_k)$ if and only if 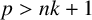$p>nk+1$.

Keywords

Berezin transformHartogs triangles

MSC classification

Primary: 32A36: Bergman spaces
Secondary: 47B35: Toeplitz operators, Hankel operators, Wiener-Hopf operators 47G30: Pseudodifferential operators
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work is supported by the Science and Technology Research Project of Hubei Provincial Department of Education, Grant No. Q20191109.

References

Axler, S. and Zheng, D., ‘Compact operators via the Berezin transform’, Indiana Univ. Math. J. 47(2) (1998), 387–400.10.1512/iumj.1998.47.1407CrossRefGoogle Scholar
Bi, E. and Hou, Z., ‘Canonical metrics on generalised Hartogs triangles’, C. R. Math. 360 (2022), 305–313.10.5802/crmath.283CrossRefGoogle Scholar
Bi, E. and Su, G., ‘Balanced metric and Berezin quantization on Hartogs triangles’, Ann. Mat. Pura Appl. (4) 200(1) (2021), 273–285.10.1007/s10231-020-00995-2CrossRefGoogle Scholar
Chakrabarti, D. and Shaw, M.-C., ‘Sobolev regularity of the $\overline{\partial}$ -equation on the Hartogs triangle’, Math. Ann. 356(1) (2013), 241–258.10.1007/s00208-012-0840-yCrossRefGoogle Scholar
Chen, L., ‘The ${L}^p$ boundedness of the Bergman projection for a class of bounded Hartogs domains’, J. Math. Anal. Appl. 448(1) (2017), 598–610.10.1016/j.jmaa.2016.11.024CrossRefGoogle Scholar
Dostanić, M., ‘Norm of Berezin transform on ${L}^p$ space’, J. Anal. Math. 104 (2008), 13–23.10.1007/s11854-008-0014-8CrossRefGoogle Scholar
Edholm, L. and McNeal, J., ‘The Bergman projection on fat Hartogs triangles: ${L}^p$ boundedness’, Proc. Amer. Math. Soc. 144(5) (2015), 2185–2196.10.1090/proc/12878CrossRefGoogle Scholar
Engliš, M., ‘Compact Toeplitz operators via the Berezin transform on bounded symmetric domains’, Integral Equations Operator Theory 33(4) (1999), 426–455.10.1007/BF01291836CrossRefGoogle Scholar
Göǧüş, N. and Şahutoǧlu, S., ‘A sufficient condition for ${L}^p$ regularity of the Berezin transform’, Complex Var. Theory Appl. 68(8) (2023), 1419–1428.10.1080/17476933.2022.2052864CrossRefGoogle Scholar
Lee, J., ‘On the Berezin transform on ${D}^n$ ’, Commun. Korean Math. Soc. 12(2) (1997), 311–324.Google Scholar
Li, H., ‘Schatten class Hankel operators on the Bergman spaces of strongly pseudoconvex domains’, Proc. Amer. Math. Soc. 119(4) (1993), 1211–1221.10.1090/S0002-9939-1993-1169879-9CrossRefGoogle Scholar
Marković, M., ‘On the Forelli–Rudin projection theorem’, Integral Equations Operator Theory 81(3) (2015), 409–425.10.1007/s00020-014-2160-yCrossRefGoogle Scholar
Qin, C., Wu, H. and Guo, X., ‘ ${L}^p$ boundedness of Forelli–Rudin type operators on the Hartogs triangle’, J. Math. Anal. Appl. 528(1) (2023), Article no. 127480, 21 pages.10.1016/j.jmaa.2023.127480CrossRefGoogle Scholar
Rudin, W., Function Theory in the Unit Ball of ${\mathbb{C}}^n$ (Springer-Verlag, New York, 1980).Google Scholar
Tao, T., Harmonic Analysis, Lecture notes at UCLA. Available online at http://www.math.ucla.edu/tao/247a.1.06f/notes2.pdf.Google Scholar
Yang, L. and Zou, Q., ‘Regularity of the Berezin transform on the elementary Reinhardt domains’, Complex Anal. Oper. Theory 18(4) (2024), Article no. 97, 12 pages.10.1007/s11785-024-01538-wCrossRefGoogle Scholar
Zhu, K., ‘Schatten class Hankel operators on the Bergman space of the unit ball’, Amer. J. Math. 113(1) (1991), 147–167.10.2307/2374825CrossRefGoogle Scholar
Zhu, K., Operator Theory in Function Spaces, Mathematical Surveys and Monographs, 138 (American Mathematical Society, Providence, RI, 2007).10.1090/surv/138CrossRefGoogle Scholar
Zou, Q., ‘A note on the Berezin transform on the generalised Hartogs triangles’, Arch. Math. 122 (2024), 531–540.10.1007/s00013-024-01971-5CrossRefGoogle Scholar