Hostname: page-component-6dbcb7884d-fw45b Total loading time: 0 Render date: 2025-02-14T08:47:26.387Z Has data issue: false hasContentIssue false
  • English
  • Français

LARGE 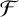$\mathcal {F}$-FREE SUBGRAPHS IN 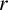$r$-CHROMATIC GRAPHS

Part of: Graph theory Extremal combinatorics

Published online by Cambridge University Press:  02 December 2022

ZHEN HE Open the ORCID record for ZHEN HE [Opens in a new window] ,
ZEQUN LV Open the ORCID record for ZEQUN LV [Opens in a new window]  and
XIUTAO ZHU Open the ORCID record for XIUTAO ZHU [Opens in a new window]
ZHEN HE
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing 100084, PR China and MTA Rényi Institute, Budapest, Hungary e-mail: [email protected]
ZEQUN LV
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing 100084, PR China and MTA Rényi Institute, Budapest, Hungary e-mail: [email protected]
XIUTAO ZHU*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, PR China and MTA Rényi Institute, Budapest, Hungary
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a graph G and a family of graphs 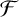$\mathcal {F}$, the Turán number 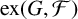${\mathrm {ex}}(G,\mathcal {F})$ is the maximum number of edges an 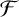$\mathcal {F}$-free subgraph of G can have. We prove that 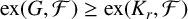${\mathrm {ex}}(G,\mathcal {F})\ge {\mathrm {ex}}(K_r, \mathcal {F})$ if the chromatic number of G is r and 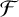$\mathcal {F}$ is a family of connected graphs. This result answers a question raised by Briggs and Cox [‘Inverting the Turán problem’, Discrete Math. 342(7) (2019), 1865–1884] about the inverse Turán number for all connected graphs.

Keywords

inverse Turán problemchromatic numberconnected graph

MSC classification

Primary: 05D05: Extremal set theory
Secondary: 05C15: Coloring of graphs and hypergraphs
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 2 , October 2023 , pp. 200 - 204
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alon, N., ‘Bipartite subgraphs’, Combinatorica 16 (1996), 301–311.10.1007/BF01261315CrossRefGoogle Scholar
Briggs, J. and Cox, C., ‘Inverting the Turán problem’, Discrete Math. 342(7) (2019), 1865–1884.10.1016/j.disc.2019.03.005CrossRefGoogle Scholar
Dowden, C., ‘Extremal ${C}_4$ -free/ ${C}_5$ -free planar graphs’, J. Graph Theory 83 (2015), 213–230.10.1002/jgt.21991CrossRefGoogle Scholar
Erdős, P., ‘On some problems in graph theory, combinatorial analysis and combinatorial number theory’, in: Graph Theory and Combinatorics (eds. Erdős, P. and Bollabás, B.) (Academic Press, London, 1984), 1–17.Google Scholar
Erdős, P. and Simonovits, M., ‘A limit theorem in graph theory’, Studia Sci. Math. Hungar. 1 (1946), 51–57.Google Scholar
Erdős, P. and Stone, A. H., ‘On the structure of linear graphs’, Bull. Amer. Math. Soc. (N.S.) 52(12) (1946), 1087–1091.10.1090/S0002-9904-1946-08715-7CrossRefGoogle Scholar
Ferneyhough, S., Haas, R., Hanson, D. and MacGillivray, G., ‘Star forests, dominating sets and Ramsey-type problems’, Discrete Math. 245(1–3) (2002), 255–262.10.1016/S0012-365X(01)00046-2CrossRefGoogle Scholar
Foucaud, F., Krivelevich, M. and Perarnau, G., ‘Large subgraphs without short cycles’, SIAM J. Discrete Math. 29(1) (2015), 65–78.10.1137/140954416CrossRefGoogle Scholar
Frankl, P. and Rödl, V., ‘Large triangle-free subgraphs in graphs without ${K}_4$ ’, Graphs Combin. 2 (1986), 135–144.10.1007/BF01788087CrossRefGoogle Scholar
Győri, E., Salia, N., Tompkins, C. and Zamora, O., ‘Inverse Turán numbers’, Discrete Math. 345 (2022), Article no. 112779.10.1016/j.disc.2021.112779CrossRefGoogle Scholar
Turán, P., ‘On an extremal problem in graph theory’, Mat. Fiz. Lapok 48 (1941), 107–111.Google Scholar
Zhu, X. T. and Chen, Y. J., ‘Inverting the Turán problem with chromatic number’, Discrete Math. 344(9) (2021), Article no. 112517.10.1016/j.disc.2021.112517CrossRefGoogle Scholar