Hostname: page-component-f554764f5-68cz6 Total loading time: 0 Render date: 2025-04-09T16:20:41.655Z Has data issue: false hasContentIssue false
  • English
  • Français

INTEGER POLYGONS OF GIVEN PERIMETER

Part of: Polytopes and polyhedra Combinatorics Algebraic combinatorics

Published online by Cambridge University Press:  30 January 2019

JAMES EAST Open the ORCID record for JAMES EAST [Opens in a new window]  and
RON NILES Open the ORCID record for RON NILES [Opens in a new window]
JAMES EAST*
Affiliation:
Centre for Research in Mathematics, Western Sydney University, Sydney, Australia email [email protected]
RON NILES
Affiliation:
Memverge Inc., San Jose, California 95134, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A classical result of Honsberger states that the number of incongruent triangles with integer sides and perimeter $n$ is the nearest integer to 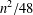$n^{2}/48$ ($n$ even) or 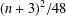$(n+3)^{2}/48$ ($n$ odd). We solve the analogous problem for 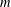$m$-gons (for arbitrary but fixed 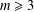$m\geq 3$) and for polygons (with arbitrary number of sides).

Keywords

enumerationinteger polygonsperimeterdihedral groupsorbit enumeration

MSC classification

Primary: 52B05: Combinatorial properties (number of faces, shortest paths, etc.)
Secondary: 05A17: Partitions of integers 05E18: Group actions on combinatorial structures 05A10: Factorials, binomial coefficients, combinatorial functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 1 , August 2019 , pp. 131 - 147
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Andrews, G. E., ‘A note on partitions and triangles with integer sides’, Amer. Math. Monthly 86(6) (1979), 477–478.Google Scholar
Andrews, G. E., Paule, P. and Riese, A., ‘MacMahon’s partition analysis. IX. k-gon partitions’, Bull. Aust. Math. Soc. 64(2) (2001), 321–329.Google Scholar
Cameron, P. J., Combinatorics: Topics, Techniques, Algorithms (Cambridge University Press, Cambridge, 1994).Google Scholar
Dickson, L. E., History of the Theory of Numbers. Vol. II: Diophantine Analysis (Chelsea, New York, 1966).Google Scholar
Hirschhorn, M. D., ‘Triangles with integer sides, revisited’, Math. Mag. 73(1) (2000), 53–56.Google Scholar
Hirschhorn, M. D., ‘Triangles with integer sides’, Math. Mag. 76(4) (2003), 306–308.Google Scholar
Honsberger, R., Mathematical Gems. III, The Dolciani Mathematical Expositions, 9 (Mathematical Association of America, Washington, DC, 1985).Google Scholar
Jenkyns, T. and Muller, E., ‘Triangular triples from ceilings to floors’, Amer. Math. Monthly 107(7) (2000), 634–639.Google Scholar
Jordan, J. H., Walch, R. and Wisner, R. J., ‘Triangles with integer sides’, Amer. Math. Monthly 86(8) (1979), 686–689.Google Scholar
Krier, N. and Manvel, B., ‘Counting integer triangles’, Math. Mag. 71(4) (1998), 291–295.Google Scholar
Marsden, M. J., ‘Triangles with integer-valued sides’, Amer. Math. Monthly 81 (1974), 373–376.Google Scholar
Phelps, R. R. and Fine, N. J., ‘Perfect triangles’, Amer. Math. Monthly 63 (1956), 43–44.Google Scholar
Singmaster, D., ‘Triangles with integer sides and sharing barrels’, College Math. J. 21(4) (1990), 278–285.Google Scholar
Subbarao, M. V., ‘Perfect triangles’, Amer. Math. Monthly 78 (1971), 384–385.Google Scholar
The Online Encyclopedia of Integer Sequences (2018), published electronically at http://oeis.org/.Google Scholar