Hostname: page-component-55f67697df-4ks9w Total loading time: 0 Render date: 2025-05-09T11:05:31.789Z Has data issue: false hasContentIssue false
  • English
  • Français

GALOIS GROUPS OF RECIPROCAL SEXTIC POLYNOMIALS

Part of: Field extensions Computational number theory

Published online by Cambridge University Press:  27 February 2023

CHAD AWTREY Open the ORCID record for CHAD AWTREY [Opens in a new window]  and
ALLY LEE
CHAD AWTREY*
Affiliation:
Department of Mathematics and Computer Science, Samford University, 800 Lakeshore Drive, Birmingham, AL 35229, USA
ALLY LEE
Affiliation:
Department of Mathematics and Computer Science, Samford University, 800 Lakeshore Drive, Birmingham, AL 35229, USA e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let F be a subfield of the complex numbers and 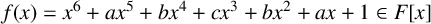$f(x)=x^6+ax^5+bx^4+cx^3+bx^2+ax+1 \in F[x]$ an irreducible polynomial. We give an elementary characterisation of the Galois group of 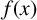$f(x)$ as a transitive subgroup of 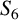$S_6$. The method involves determining whether three expressions involving a, b and c are perfect squares in F and whether a related quartic polynomial has a linear factor. As an application, we produce one-parameter families of reciprocal sextic polynomials with a specified Galois group.

Keywords

reciprocal polynomialssexticGalois group

MSC classification

Primary: 12F10: Separable extensions, Galois theory
Secondary: 11Y40: Algebraic number theory computations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 1 , February 2024 , pp. 37 - 44
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Altmann, A., Awtrey, C., Cryan, S., Shannon, K. and Touchette, M., ‘Galois groups of doubly even octic polynomials’, J. Algebra Appl. 19(1) (2020), Article no. 2050014.CrossRefGoogle Scholar
Awtrey, C. and Jakes, P., ‘Galois groups of even sextic polynomials’, Canad. Math. Bull. 63(3) (2020), 670–676.CrossRefGoogle Scholar
Butler, G. and McKay, J., ‘The transitive groups of degree up to eleven’, Comm. Algebra 11(8) (1983), 863–911.CrossRefGoogle Scholar
Dickson, L. E., ‘The Galois group of a reciprocal quartic equation’, Amer. Math. Monthly 15(4) (1908), 71–78.CrossRefGoogle Scholar
Dixon, J. D. and Mortimer, B., Permutation Groups, Graduate Texts in Mathematics, 163 (Springer-Verlag, New York, 1996).CrossRefGoogle Scholar
Jones, L., ‘Infinite families of reciprocal monogenic polynomials and their Galois groups’, New York J. Math. 27 (2021), 1465–1493.Google Scholar
Jones, L., ‘Sextic reciprocal monogenic dihedral polynomials’, Ramanujan J. 56(3) (2021), 1099–1110.CrossRefGoogle Scholar
Lindstrom, P., Galois Theory of Palindromic Polynomials, Master’s Thesis, University of Oslo, Spring, 2015.Google Scholar
Soicher, L. and McKay, J., ‘Computing Galois groups over the rationals’, J. Number Theory 20(3) (1985), 273–281.CrossRefGoogle Scholar
Stauduhar, R. P., ‘The determination of Galois groups’, Math. Comp. 27 (1973), 981–996.CrossRefGoogle Scholar
The GAP Group, GAP – Groups, Algorithms, and Programming, Version 4.6.5, 2013, available online at http://www.gap-system.org.Google Scholar